题目内容
对于正数x,规定f(x)=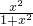 .
.
(1)计算f(2)=______,f( )=______,f(2)+f(
)=______,f(2)+f( )=______,f(3)+f(
)=______,f(3)+f( )=______,…;
)=______,…;
(2)猜想f(x)+ =______,请予以证明.
=______,请予以证明.
(3)现在你会计算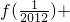
 +
+ +…f(
+…f( )+f(
)+f( )+f(1)+f(2)+f(3)+…+f(2010)+f(2011)+f(2012)的值了吗,写出你的计算过程.
)+f(1)+f(2)+f(3)+…+f(2010)+f(2011)+f(2012)的值了吗,写出你的计算过程.
解:(1)由规定运算可知,f(2)= =
= ,f(
,f( )=
)= =
= ,
,
则f(2)+f( )=
)= +
+ =1,f(3)+f(
=1,f(3)+f( )=
)= +
+ =
= +
+ =1,
=1,
故答案为: ,
, ,1,1;
,1,1;
(2)f(x)+f( )=
)=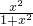 +
+ =
=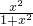 +
+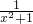 =1,
=1,
故答案为:1;
(3)f( )+f(
)+f( )+f(
)+f( )+…+f(
)+…+f( )+f(
)+f( )+f(1)+f(2)+f(3)+…+f(2010)+f(2011)+f(2012)
)+f(1)+f(2)+f(3)+…+f(2010)+f(2011)+f(2012)
=f(1)+[f( )+f(2)]+[f(
)+f(2)]+[f( )+f(3)+]+…+[f(
)+f(3)+]+…+[f( )+f(2012)]
)+f(2012)]
= +1+1+…+1=2011
+1+1+…+1=2011 .
.
分析:(1)把x的值代入规定的分式计算即可;
(2)由(1)猜想一般结论,把 代替规定算式中的x,进行分式加减运算即可;
代替规定算式中的x,进行分式加减运算即可;
(3)根据(2)得出的规律,分组计算.
点评:本题考查了分式的加减法.分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可;如果是异分母分式,则必须先通分,把异分母分式化为同分母分式,然后再相加减.
 =
= ,f(
,f( )=
)= =
= ,
,则f(2)+f(
 )=
)= +
+ =1,f(3)+f(
=1,f(3)+f( )=
)= +
+ =
= +
+ =1,
=1,故答案为:
 ,
, ,1,1;
,1,1;(2)f(x)+f(
 )=
)=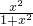 +
+ =
=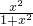 +
+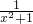 =1,
=1,故答案为:1;
(3)f(
 )+f(
)+f( )+f(
)+f( )+…+f(
)+…+f( )+f(
)+f( )+f(1)+f(2)+f(3)+…+f(2010)+f(2011)+f(2012)
)+f(1)+f(2)+f(3)+…+f(2010)+f(2011)+f(2012)=f(1)+[f(
 )+f(2)]+[f(
)+f(2)]+[f( )+f(3)+]+…+[f(
)+f(3)+]+…+[f( )+f(2012)]
)+f(2012)]=
 +1+1+…+1=2011
+1+1+…+1=2011 .
.分析:(1)把x的值代入规定的分式计算即可;
(2)由(1)猜想一般结论,把
 代替规定算式中的x,进行分式加减运算即可;
代替规定算式中的x,进行分式加减运算即可;(3)根据(2)得出的规律,分组计算.
点评:本题考查了分式的加减法.分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可;如果是异分母分式,则必须先通分,把异分母分式化为同分母分式,然后再相加减.

练习册系列答案
相关题目
 (1)对于正数x,规定f(x)=
(1)对于正数x,规定f(x)=