题目内容
7.解不等式组,在数轴上表示出来,并写出不等式组的整数解.$\left\{\begin{array}{l}{3(x+1)>4x+2}\\{\frac{x}{2}≥\frac{x-1}{3}}\end{array}\right.$.
分析 先求出每个不等式的解集,再求出不等式组的解集,即可求出答案.
解答 解:$\left\{\begin{array}{l}{3(x+1)>4x+2①}\\{\frac{x}{2}≥\frac{x-1}{3}②}\end{array}\right.$
∵解不等式①得:x<1,
解不等式②得:x≥-2,
∴不等式组的解集为-2≤x<1,
在数轴上表示不等式组的解集为: ,
,
∴不等式组的整数解为-2,-1,0.
点评 本题考查了解一元一次不等式(组),在数轴上表示不等式组的解集,不等式组的整数解的应用,能根据不等式的解集求出不等式组的解集是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.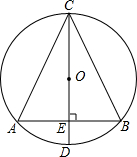 如图,⊙O中,直径CD垂直于弦AB于E,AB=2,连接AC,BC,则tan∠ACB的值的倒数等于线段( )
如图,⊙O中,直径CD垂直于弦AB于E,AB=2,连接AC,BC,则tan∠ACB的值的倒数等于线段( )
 如图,⊙O中,直径CD垂直于弦AB于E,AB=2,连接AC,BC,则tan∠ACB的值的倒数等于线段( )
如图,⊙O中,直径CD垂直于弦AB于E,AB=2,连接AC,BC,则tan∠ACB的值的倒数等于线段( )| A. | AC的长 | B. | AE的长 | C. | OE的长 | D. | CE的长 |
16.将直线y=-3x+1沿y轴向上平移3个单位,得图象的函数解析式为( )
| A. | y=-3x-2 | B. | y=-3x+4 | C. | y=-3x-1 | D. | y=-3x |
 如图,在Rt△ACB中,∠C=90°,AB=10、BC=6,分别以AB、BC、AC为直径作三个半圆,求阴影部分的面积.
如图,在Rt△ACB中,∠C=90°,AB=10、BC=6,分别以AB、BC、AC为直径作三个半圆,求阴影部分的面积. 有理数m,n在数轴上的位置如图所示,则下列关系中正确的序号是(2).
有理数m,n在数轴上的位置如图所示,则下列关系中正确的序号是(2).