题目内容
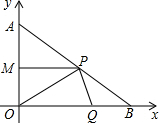
如图，在Rt△AOB中，点A是直线y=x+m与双曲线y=| m | x |
4
4
．分析：设A的坐标是（a，b），得出b=a+m，b=
，推出m=ab，根据△AOB的面积求出ab的值，代入求出m即可．
| m |
| a |
解答：解：
设A的坐标是（a，b），则a＞0，b＞0，
∵A是直线y=x+m与双曲线y=
在第一象限的交点，
∴b=a+m，b=
，
即m=ab，
∵S△AOB=2，
∴
OB×AB=2，
∴
ab=2，
即ab=4，
∴m=ab=4，
故答案为：4．
解：设A的坐标是（a，b），则a＞0，b＞0，
∵A是直线y=x+m与双曲线y=
| m |
| x |
∴b=a+m，b=
| m |
| a |
即m=ab，
∵S△AOB=2，
∴
| 1 |
| 2 |
∴
| 1 |
| 2 |
即ab=4，
∴m=ab=4，
故答案为：4．
点评：本题考查了一次函数与反比例函数的交点问题和三角形的面积的应用，关键是能把已知量和未知量结合起来，题型比较好，具有一定的代表性．
练习册系列答案
相关题目
分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动，速度均为1cm/秒，设P、Q移动时间为t（0≤t≤4）
如图，在Rt△AOB中，∠ABO=90°，OB=4，AB=8，且反比例函数
（2013•咸宁）如图，在Rt△AOB中，OA=OB=3
（2013•南岗区一模）如图，在Rt△AOB中，∠AOB=90°，且AO=8，BO=6，P是线段AB上一个动点，PE⊥A0于E，PF⊥B0于F．设