题目内容
19.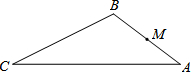 如图,已知△ABC中,AB=2$\sqrt{5}$,AC=4$\sqrt{5}$,BC=6.点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,则线段MN的长=3或$\frac{3}{2}$.
如图,已知△ABC中,AB=2$\sqrt{5}$,AC=4$\sqrt{5}$,BC=6.点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,则线段MN的长=3或$\frac{3}{2}$.
分析 分别从当$\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}$时,△AMN∽△ABC与当$\frac{AM}{AC}=\frac{AN}{AB}=\frac{MN}{BC}$时,△AMN∽△ACB,去分析求解即可求得答案.
解答 解:∵△ABC中,AB=2$\sqrt{5}$,AC=4$\sqrt{5}$,BC=6.点M为AB的中点,
∴AM=$\sqrt{5}$,
∴当$\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}$时,△AMN∽△ABC,
即$\frac{MN}{6}$=$\frac{1}{2}$,
解得:MN=3;
当$\frac{AM}{AC}=\frac{AN}{AB}=\frac{MN}{BC}$时,△AMN∽△ACB,
即$\frac{MN}{6}=\frac{\sqrt{5}}{4\sqrt{5}}$,
解得:MN=$\frac{3}{2}$,
∴MN=3或$\frac{3}{2}$.
故答案为:3或$\frac{3}{2}$.
点评 此题考查了相似三角形的判定.注意从△AMN∽△ABC与△AMN∽△ACB两方面去分析求解.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
10.下列二次根式为最简二次根式的是( )
| A. | $\sqrt{4}$ | B. | $\sqrt{6}$ | C. | $\sqrt{12}$ | D. | $\sqrt{\frac{1}{2}}$ |
7.烟草是全球第二个主要死亡因素,每年大约导致500万人死亡,在中国每年有120万人因吸烟而死亡,占全球吸烟有关疾病死亡人数的$\frac{1}{4}$.同时,科学证明,被动吸烟者吸入烟雾受到的危害高于吸烟者.烟雾中含有焦油、砷、铅、汞等致病物质.2010年3月1日,《杭州市公共场所控制吸烟条例》正式实施,杭州市因此成为我省首个公共场所实行控烟的地市.这一举措让很多杭州人收益,假定杭州有43万烟民平均每年用于吸烟的费用为2000元,你知道这笔费用是多少吗?用科学记数法表示为( )
| A. | 86×107 | B. | 8.6×109 | C. | 8.6×108 | D. | 0.86×109 |
8.如果$\sqrt{(x-2)(x-3)}$=$\sqrt{(x-2)}$•$\sqrt{(x-3)}$成立,则( )
| A. | x≥2 | B. | x≥3 | C. | 2≤x≤3 | D. | x=0 |