题目内容
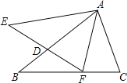
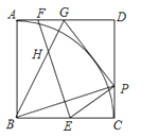
【题目】如图，在菱形
中，
，
，点
是边
边的中点，点
、
分别是
、
上的两个动点，则
的最小值是________．
【答案】
【解析】
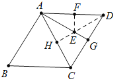
作DH⊥AC垂足为H与AG交于点E，点H关于AG的对称点为F，此时EF+ED最小=DH，先证明△ADC是等边三角形，在RT△DCH中利用勾股定理即可解决问题．
作DH⊥AC垂足为H与AG交于点E，
∵四边形ABCD是菱形，
∵AB=AD=CD=BC=6，
∵∠B=60°，
∴∠ADC=∠B=60°，
∴△ADC是等边三角形，
∵AG是中线，
∴∠GAD=∠GAC，
∴点H关于AG的对称点F在AD上，此时EF+ED最小=DH．
在RT△DHC中，∵∠DHC=90°，DC=6，∠CDH=
∠ADC=30°，
∴CH=DC=3，DH=
=
=3
，
∴EF+DE的最小值=DH=3，
故答案为：3．
练习册系列答案
相关题目
