题目内容
14.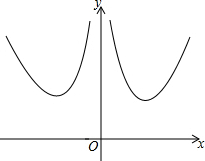 函数y=x2+$\frac{4}{{x}^{2}}$的图象如图所示,关于该函数下列结论正确的是①②③(填序号).
函数y=x2+$\frac{4}{{x}^{2}}$的图象如图所示,关于该函数下列结论正确的是①②③(填序号).①函数图象经过点(-2,5);
②函数可取得最小值;
③方程x2+$\frac{4}{{x}^{2}}$=5有4个解;
④不等式x2+$\frac{4}{{x}^{2}}$≤5的解集为1≤x≤2.
分析 ①把x=-2代入y=x2+$\frac{4}{{x}^{2}}$可得函数图象经过点(-2,5),故①正确;
②根据函数图象有最低点,可得函数有最小值,故②正确;
③解方程可得有4个解,故③正确;
④解出等式x2+$\frac{4}{{x}^{2}}$≤5的解集是-2≤x≤-1或1≤x≤2,于是判断故④错误,
解答 解:①当x=-2时,y=(-2)2$+\frac{4}{(-2)^{2}}$=5,
∴函数图象经过点(-2,5),故①正确;
②∵由图象知:函数图象有最低点,
∴函数可取得最小值,故②正确;
③解方程x2+$\frac{4}{{x}^{2}}$=5得:x=±1,x=±2,
∴方程x2+$\frac{4}{{x}^{2}}$=5有4个解,故③正确;
④等式x2+$\frac{4}{{x}^{2}}$≤5的解集为:-2≤x≤-1或1≤x≤2,
故④错误,
故答案为:①②③.
点评 本题考查了二次函数与不等式,二次函数的图象和最值,正确的识别图象是解题的关键.

练习册系列答案
相关题目
4.-|-2|的相反数的倒数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
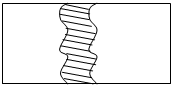 如图所示,在一块长为a米,宽为b米的长方形地上,有一条弯曲的柏油马路,马路任何地方的水平宽度都是2米,其他部分都是草地.求草地的面积.
如图所示,在一块长为a米,宽为b米的长方形地上,有一条弯曲的柏油马路,马路任何地方的水平宽度都是2米,其他部分都是草地.求草地的面积.
 如图,一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于点P,点P在第一象限,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、D,且S△PBD=4,$\frac{OD}{BD}$=$\frac{1}{2}$.
如图,一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于点P,点P在第一象限,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、D,且S△PBD=4,$\frac{OD}{BD}$=$\frac{1}{2}$.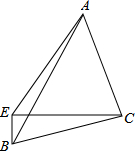 如图,△ABC中,AC=BC,∠BCA=90°,E为△ABC外一点,连结AE、BE、CE,若∠BEC=90°,AE=$\sqrt{13}$BE,则tan∠BCE=$\frac{1}{3}$.
如图,△ABC中,AC=BC,∠BCA=90°,E为△ABC外一点,连结AE、BE、CE,若∠BEC=90°,AE=$\sqrt{13}$BE,则tan∠BCE=$\frac{1}{3}$.