题目内容
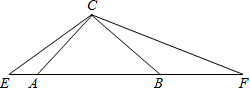 如图,已知∠ACB=90°,AC=BC,∠ECF=135°,当AB=
如图,已知∠ACB=90°,AC=BC,∠ECF=135°,当AB= 时.
时.
(1)求证:△ACE∽△BFC;
(2)求AE•BF的值.
(1)证明:∵∠ACB=90°,AC=BC,∠ECF=135°,
∴∠CAB=∠CBA=45°,∠ECA+∠FCB=45°.
∵∠E+∠ECA=∠CAB=45°(三角形外角定理),
∴∠E=∠FCB.
又∵∠CAE=∠FBC,
∴△ACE∽△BFC;
(2)∵在直角△ABC中,AC=BC,AB= ,
,
∴AC=BC=1.
∵△ACE∽△BFC,
∴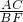 =
= ,
,
∴AE•BF=AC•BC=1×1=1,即AE•BF的值为1.
分析:(1)根据等腰直角三角形的性质、三角形外角定理以及补角的定义证得∠E=∠FCB,∠CAE=∠FBC,所以△ACE∽△BFC;
(2)利用勾股定理在等腰直角三角形ABC中求得AC=BC=1;然后由(1)中的△ACE∽△BFC的对应边成比例列出比例式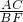 =
= ,所以易求AE•BF的值.
,所以易求AE•BF的值.
点评:本题考查了相似三角形的判定与性质.本题通过△ACE和△BFC中的两组对应角相等来证明这两个三角形相似的.
∴∠CAB=∠CBA=45°,∠ECA+∠FCB=45°.
∵∠E+∠ECA=∠CAB=45°(三角形外角定理),
∴∠E=∠FCB.
又∵∠CAE=∠FBC,
∴△ACE∽△BFC;
(2)∵在直角△ABC中,AC=BC,AB=
 ,
,∴AC=BC=1.
∵△ACE∽△BFC,
∴
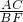 =
= ,
,∴AE•BF=AC•BC=1×1=1,即AE•BF的值为1.
分析:(1)根据等腰直角三角形的性质、三角形外角定理以及补角的定义证得∠E=∠FCB,∠CAE=∠FBC,所以△ACE∽△BFC;
(2)利用勾股定理在等腰直角三角形ABC中求得AC=BC=1;然后由(1)中的△ACE∽△BFC的对应边成比例列出比例式
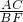 =
= ,所以易求AE•BF的值.
,所以易求AE•BF的值.点评:本题考查了相似三角形的判定与性质.本题通过△ACE和△BFC中的两组对应角相等来证明这两个三角形相似的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知∠ACB=∠CBD=90°,BC=a,AC=b,当CD=( )时,△CDB∽△ABC.
如图,已知∠ACB=∠CBD=90°,BC=a,AC=b,当CD=( )时,△CDB∽△ABC.A、
| ||||
B、
| ||||
C、
| ||||
D、
|

 如图,已知∠ACB=∠BDA=90°,要使△ABC≌△BAD,还需要添加一个条件,这个条件可以是
如图,已知∠ACB=∠BDA=90°,要使△ABC≌△BAD,还需要添加一个条件,这个条件可以是
 如图,已知∠ACB=90°,∠DAB=70°,AC平分∠DAB,∠1=35°.
如图,已知∠ACB=90°,∠DAB=70°,AC平分∠DAB,∠1=35°.