题目内容
4. 如图,△ABC≌△ADE,∠EAB=125°,∠CAD=25°,求∠BFD的度数.
如图,△ABC≌△ADE,∠EAB=125°,∠CAD=25°,求∠BFD的度数.
分析 根据全等三角形的性质求出∠EAD=∠CAB,∠B=∠D,求出∠∠EAC=∠DAB=50°,根据三角形内角和定理求出∠BFD=∠DAB,代入求出即可.
解答 解:∵△ABC≌△ADE,
∴∠EAD=∠CAB,∠B=∠D,
∴∠EAD-∠CAD=∠CAB-∠CAD,
∴∠∠EAC=∠DAB,
∵∠EAB=125°,∠CAD=25°,
∴∠DAB=∠EAC=$\frac{1}{2}×$(125°-25°)=50°,
∵∠B=∠D,∠FGD=∠BGA,∠D+∠BFD+∠FGD=180°,∠B+∠DAB+∠AGB=180°,
∴∠BFD=∠DAB=50°.
点评 本题考查了全等三角形的性质,三角形内角和定理的应用,能根据全等三角形的性质求出∠EAD=∠CAB,∠B=∠D是解此题的关键,注意:全等三角形的对应角相等,对应边相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
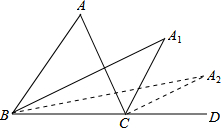 如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2014BC和∠A2014CD的平分线交于点A2015,则∠A2015=$\frac{m}{{2}^{2015}}$度.
如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2014BC和∠A2014CD的平分线交于点A2015,则∠A2015=$\frac{m}{{2}^{2015}}$度. 如图,在△ABC中,∠C=90°,DE垂直平分AB,∠CBE:∠A=1:2,则∠A=36°.
如图,在△ABC中,∠C=90°,DE垂直平分AB,∠CBE:∠A=1:2,则∠A=36°.
 现有大小相同的正方形纸片若干张,小明想用其中的3张拼成一个如图所示的长方形,小芳也想拼一个与它形状相同但比它大的长方形,则她最少要用12张正方形纸片(每个正方形纸片不得剪开).
现有大小相同的正方形纸片若干张,小明想用其中的3张拼成一个如图所示的长方形,小芳也想拼一个与它形状相同但比它大的长方形,则她最少要用12张正方形纸片(每个正方形纸片不得剪开).