题目内容
3.如图,在Rt△ABC中,∠C=90°,AB=10cm,AC=6cm,动点P从点B出发沿射线BC以2cm/s的速度移动,设运动的时间为t秒.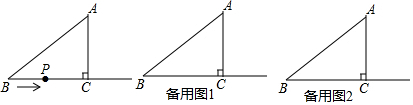
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值.
分析 (1)直接根据勾股定理求出BC的长度;
(2)当△ABP为直角三角形时,分两种情况:①当∠APB为直角时,②当∠BAP为直角时,分别求出此时的t值即可;
(3)当△ABP为等腰三角形时,分三种情况:①当AB=BP时;②当AB=AP时;③当BP=AP时,分别求出BP的长度,继而可求得t值.
解答 解:(1)在Rt△ABC中,BC2=AB2-AC2=102-62=64,
∴BC=8(cm);
(2)由题意知BP=tcm,
①当∠APB为直角时,点P与点C重合,BP=BC=8cm,即t=4;
②当∠BAP为直角时,BP=tcm,CP=(t-8)cm,AC=6cm,
在Rt△ACP中,
AP2=62+(t-8)2,
在Rt△BAP中,AB2+AP2=BP2,
即:102+[62+(t-8)2]=t2,
解得:t=$\frac{25}{4}$,
故当△ABP为直角三角形时,t=4或t=$\frac{25}{4}$;
(3)①当AB=BP时,t=5;
②当AB=AP时,BP=2BC=16cm,t=8;
③当BP=AP时,AP=BP=tcm,CP=|t-8|cm,AC=6cm,
在Rt△ACP中,AP2=AC2+CP2,
所以t2=62+(t-8)2,
解得:t=$\frac{25}{8}$,
综上所述:当△ABP为等腰三角形时,t=5或t=8或t=$\frac{25}{8}$.
点评 本题考查了勾股定理以及等腰三角形的知识,解答本题的关键是掌握勾股定理的应用,以及分情况讨论,注意不要漏解.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
18.阳光实验学校组织学生到新兴陶瓷厂参观陶瓷工艺制作,爱动脑筋的小强同学看到桌子上整齐地摆放着若干相同规格的碟子,通过测量发现碟子的个数与碟子的高度的关系如下表:
(1)当桌子上放有x个碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)桌面上整齐地摆放几摞碟子,分别从三个方向上看,其三种形状图如下图所示,小强如果想把它们整齐叠成一摞,请你求出叠成一摞后的高度.
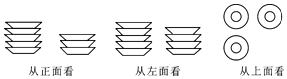
| 碟子的个数 | 碟子的高度(单位:cm) |
| 1 | 2 |
| 2 | 2+1.5 |
| 3 | 2+3 |
| 4 | 2+4.5 |
| … | … |
(2)桌面上整齐地摆放几摞碟子,分别从三个方向上看,其三种形状图如下图所示,小强如果想把它们整齐叠成一摞,请你求出叠成一摞后的高度.

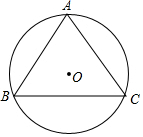 求正三角形的内切圆半径、外接圆半径和高的比.
求正三角形的内切圆半径、外接圆半径和高的比.