题目内容
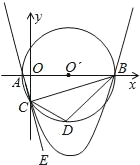
如图，已知点A的坐标是（﹣1，0），点B的坐标是（9，0），以AB为直径作⊙O′，交y轴的负半轴于点C，连接AC，BC，过A，B，C三点作抛物线．
（1）求抛物线的解析式；
（2）点E是AC延长线上一点，∠BCE的平分线CD交⊙O′于点D，连接BD，求直线BD的解析式；
（3）在（2）的条件下，抛物线上是否存在点P，使得∠PDB=∠CBD？如果存在，请求出点P的坐标；如果不存在，请说明理由．
第三问改成，在（2）的条件下，点P是直线BC下方的抛物线上一动点，当点P运动到什么位置时，△PCD的面积是△BCD面积的三分之一，求此时点P的坐标．
练习册系列答案
相关题目
在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表：
成绩/m | 1.50 | 1.55 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数/人 | 1 | 2 | 2 | 2 | 3 | 4 | 1 |
则这些运动员成绩的众数和中位数分别是（ ）
A. 2和1.65 B. 2和1.70 C. 1.75和1.65 D. 1.75和1.70
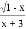有意义，则x的取值范围是______
