Question

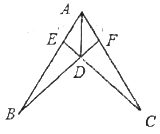
【题目】附加题：（1）已知：如图①，在和中，OA=OB，OC=OD，，求证：①AC=BD；②．

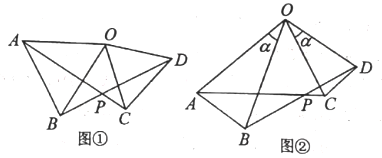
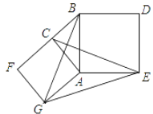
（2）如图②，在和中，若OA=OB，OC=OD，，则AC与BD间的等量关系式为 ；的大小为 ．

Answer 1

【答案】（1）见解析；（2），

【解析】

（1）①求出∠AOC=∠BOD，证出△AOC≌△BOD，根据全等三角形的性质推出即可；

②根据△AOC≌△BOD推出∠OAC=∠OBD，再利用角的和差即可求出∠APB的度数；

（2）求出∠AOC=∠BOD，证出△AOC≌△BOD，根据全等三角形的性质推出即可；根据△AOC≌△BOD推出∠OAC=∠OBD，再利用角的和差即可求出求出∠APB．

（1）证明：

①∵∠AOB=∠COD=60°，

∴∠AOB+∠BOC=∠COD+∠BOC，

∴∠AOC=∠BOD，

又∵OA＝OB，OC＝OD，

∴△AOC≌△BOD（SAS），

∴AC=BD；

②由①得：∵△AOC≌△BOD，

∴∠OAC=∠OBD，

∴∠OAC+∠AOB=∠OBD+∠APB，

∴∠OAC+60°=∠OBD+∠APB，

∴∠APB=60°；

（2）∵∠AOB=∠COD，

∴∠AOC=∠BOD，

又∵OA＝OB，OC＝OD，

∴△AOC≌△BOD（SAS），

∴AC=BD；

∵△AOC≌△BOD，

∴∠OAC=∠OBD，

∴∠OAC+∠AOB=∠OBD+∠APB，

∴∠OAC+=∠OBD+∠APB，

∴∠APB=；

故答案为：，．