Question

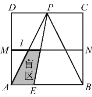
【题目】如图，分别以的直角边和斜边为边向外作正方形和正方形，连结、、．给出下列结论：

①；

②

③

④其中正确的是（ ）

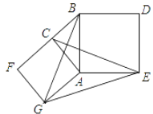
A.②③④B.①②③C.①②④D.①②③④

Answer 1

【答案】C

【解析】

利用SAS证明△AGB≌△ACE，即可判断①；证明∠BNM=∠MAE=90，即可判断②；假设③成立，利用勾股定理对等式变形证得=，而与不一定相等，即可判断③；利用勾股定理证得，从而证得结论④成立．

∵四边形和四边形都是正方形，

∴AC=AG，AB=AE，

∵∠CAG=∠BAE=90°，
∴∠CAG+∠BAC=∠BAE+∠BAC，即∠GAB=∠CAE，
在△AGB和△ACE中，

∵，

∴△AGB≌△ACE(SAS)，

∴GB=CE，故①正确；

设BA、CE相交于点M，

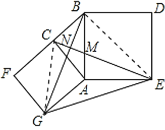
∵△AGB≌△ACE，

∴∠GBA=∠CEA，

又∵∠BMN=∠EMA，

∴∠BNM=∠MAE=90，

∴，故②正确；

设正方形和正方形的边长分别为和,

∵为直角三角形，且为斜边，

∴，

假设成立，

则有，

整理得：，即，

∴，即，

∵与不一定相等，

∴假设不成立，故③不正确；

连接CG，BE，设BG、CE相交于N，

∵，

∴，

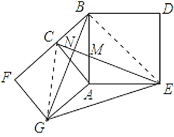
∵四边形和四边形都是正方形，

∴，，

∴，故④正确；

综上，①②④正确，