Question

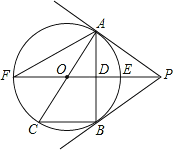
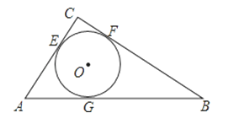
【题目】在Rt△ABC中，∠C=90°，AC=3，BC=4，AB=5．如图，⊙O是△ABC的内切圆，与三边分别相切于点E、F、G．

（1）求证：内切圆的半径r=1；

（2）求tan∠OAG的值．

Answer 1

【答案】（1）证明见解析（2）

【解析】

（1）如图连结OE，OF，OG．由 O是△ABC的内切圆，∠C=90°，得到四边形CEOF是正方形，根据切线长定理列方程得到结果；
（2）连结OA，在Rt△AOG中，由锐角三角函数得到结果．

（1）证明：如图连结OE，OF，OG．

∵⊙O是△ABC的内切圆，∠C=90°，

∴四边形CEOF是正方形，

∴CE=CF=r．

又∵AG=AE=3﹣r，BG=BF=4﹣r，AG+BG=5，

∴（3﹣r）+（4﹣r）=5．

解得r=1；

（2）解：连结OA，在Rt△AOG中，

∵r=1，AG=3﹣r=2，

tan∠OAG=．