题目内容
11.在△ABC中,a,b,c为其三边长,且a:b:c=5:13:12,试判断△ABC是否为直角三角形.分析 由a:b:c=5:13:12,不妨设a=5x,b=13x,c=12x,进一步利用勾股定理的逆定理两条小边的平方和是否等于最长边的平方判定即可.
解答 解:∵a:b:c=5:13:12,
设a=5x,b=13x,c=12x,
(5x)2=25x2,(13x)2=169x2,(12x)2=144x2;
25x2+144x2=169x2,
即a2+c2=b2,
∴△ABC是直角三角形.
点评 此题主要考查了勾股定理逆定理,关键是掌握勾股定理的逆定理:已知△ABC的三边满足a2+b2=c2,则△ABC是直角三角形.

练习册系列答案
相关题目
1.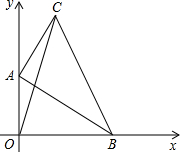 如图,在平面直角坐标系中,Rt△ABC的直角顶点A和顶点B分别在y轴正半轴及x轴正半轴上运动,若AB=4,AC=3,则在运动过程中,线段OC的最大值是( )
如图,在平面直角坐标系中,Rt△ABC的直角顶点A和顶点B分别在y轴正半轴及x轴正半轴上运动,若AB=4,AC=3,则在运动过程中,线段OC的最大值是( )
 如图,在平面直角坐标系中,Rt△ABC的直角顶点A和顶点B分别在y轴正半轴及x轴正半轴上运动,若AB=4,AC=3,则在运动过程中,线段OC的最大值是( )
如图,在平面直角坐标系中,Rt△ABC的直角顶点A和顶点B分别在y轴正半轴及x轴正半轴上运动,若AB=4,AC=3,则在运动过程中,线段OC的最大值是( )| A. | 5 | B. | 2+$\sqrt{13}$ | C. | $\sqrt{13}$ | D. | 6 |
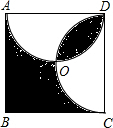 如图,分别以正方形ABCD的边AD和DC为直径画两个半圆交于点O,若正方形的边长为10cm,求阴影部分的面积.
如图,分别以正方形ABCD的边AD和DC为直径画两个半圆交于点O,若正方形的边长为10cm,求阴影部分的面积.