Question

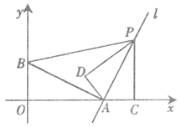
【题目】在平面直角坐标系中，已知抛物线.

（1）当时，

①抛物线的对称轴为________；

②若在抛物线上有两点，且，则的取值范围是________；

（2）抛物线的对称轴与轴交于点，点与点关于轴对称，将点向右平移3个单位得到点，若抛物线与线段恰有一个公共点，结合图象，求的取值范围.

Answer 1

【答案】（1）①1；②或；（2）或.

【解析】

（1）①根据抛物线的对称轴公式即可求得；

②根据抛物线的对称性质，求得点的对称点为，根据函数图象即可求得答案；

（2）根据平移的性质，分别求得A、B的坐标，依题意，根据函数图象，三种情况分类讨论，得出相应的a值，从而得结论．

（1）①抛物线的对称轴为：；

②∵抛物线关于对称，

∴点的对称点为，

∵，

∴抛物线开口向上，

观察图象，或时，；

故答案为：①1；②或；

（2）∵抛物线的对称轴为，且对称轴与轴交于点，

∴点的坐标为，

∵点与点关于轴对称，

∴点的坐标为，

∵点右移3个单位得到点，

∴点的坐标为，

依题意，抛物线与线段恰有一个公共点，

把点代入可得；

把点代入可得；

把点代入可得．

根据所画图象可知抛物线与线段恰有一个公共点时可得或．