Question

16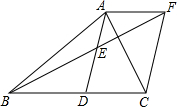．如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作AF∥BC，交BE的延长线于点F，连接CF．
（1）求证：①△AEF≌△DEB；
②四边形ADCF是平行四边形．
（2）若AB=AC，∠BAC=90°，试判断四边形ADCF的形状：正方形（不要求证明）．

Answer 1

分析 （1）①由AF∥BC得∠AFE=∠EBD，继而结合∠AEF=∠DEB、AE=DE即可判定全等；
②由①中结论可得AF=BD，根据中线性质可得AF=BD=CD，结合AF∥BC即可得出四边形ADCF是平行四边形；
（2）根据AB=AC、∠BAC=90°且AD是BC边上的中线可得AD=CD、∠ADC=90°，由四边形ADCF是平行四边形可得答案．

解答 解：（1）①证明：∵AF∥BC，
∴∠AFE=∠EBD，
∵E是AD的中点，
∴AE=DE．  
在△AEF和△DEB中
∵$\left\{\begin{array}{l}{∠AFE=∠DBE}\\{∠AEF=∠DEB}\\{AE=DE}\end{array}\right.$，
∴△AEF≌△DEB（AAS）．    
②∵△AEF≌△DEB，
∴AF=BD． 
又∵BD=DC                  
∴AF=DC．
又∵AF∥BC，
∴四边形ADCF为平行四边形；

（2）∵AB=AC、∠BAC=90°，且AD为BC边的中线，
∴AD=CD=BD，AD⊥BC，即∠ADC=90°，
∵四边形ADCF为平行四边形，
∴四边形ADCF为正方形，
故答案为：正方形．

点评 此题主要考查了平行四边形的判定以及全等三角形的判定与性质、正方形的判定、三角形中线的性质等知识点，熟练掌握平行四边形的判定是解题关键．