题目内容
17.在关于x,y的二元一次方程组$\left\{\begin{array}{l}{x+2y=2a}\\{2x-y=1}\end{array}\right.$中.(1)若a=3,求方程组的解;
(2)若S=a(3x+y),当a为何值时,S有最值?
分析 (1)把a=3代入,再解方程组即可;
(2)两方程相加,代入后得出S=a(2a+1),化成顶点式,即可得出答案.
解答 解:(1)把a=3代入得:$\left\{\begin{array}{l}{x+2y=6①}\\{2x-y=1②}\end{array}\right.$
①+②×2得:5x=8,
x=$\frac{8}{5}$,
①×2-②得:5y=11,
y=$\frac{11}{5}$,
所以方程组的解为:$\left\{\begin{array}{l}{x=\frac{8}{5}}\\{y=\frac{11}{5}}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x+2y=2a①}\\{2x-y=1②}\end{array}\right.$
①+②得:3x+y=2a+1,
∵S=a(3x+y),
∴S=a(2a+1)=2a2+a=2(a+$\frac{1}{4}$)2+$\frac{1}{8}$,
当a=-$\frac{1}{4}$时,S有最小值.
点评 本题考查了解二元一次方程组,二次函数的最值的应用,能正确解二元一次方程组是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7. 如图,在⊙O中,弦AB、CD相交于P,若∠A=30°,∠APD=60°,则∠B等于( )
如图,在⊙O中,弦AB、CD相交于P,若∠A=30°,∠APD=60°,则∠B等于( )
 如图,在⊙O中,弦AB、CD相交于P,若∠A=30°,∠APD=60°,则∠B等于( )
如图,在⊙O中,弦AB、CD相交于P,若∠A=30°,∠APD=60°,则∠B等于( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
8.下列计算错误的是( )
| A. | (a-1b2)3=$\frac{{b}^{6}}{{a}^{3}}$ | B. | (a2b-2)-3=$\frac{{b}^{6}}{{a}^{6}}$ | ||
| C. | (-3ab-1)3=-$\frac{{a}^{3}}{27{b}^{3}}$ | D. | (2m2n-2)2•3m-3n3=$\frac{12m}{n}$ |
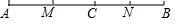 (1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,M,N分别是AC,BC的中点,求线段MN的长度.
(1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,M,N分别是AC,BC的中点,求线段MN的长度. 已知如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠A=22.5°,CD=8cm,求⊙O的半径.
已知如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠A=22.5°,CD=8cm,求⊙O的半径.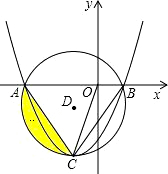 已知:如图,抛物线y=ax2+bx+c的顶点C在以D(-3,-3)为圆心,6为半径的圆上,且经过⊙D与x轴的两个交点A、B,连结AC、BC、OC.
已知:如图,抛物线y=ax2+bx+c的顶点C在以D(-3,-3)为圆心,6为半径的圆上,且经过⊙D与x轴的两个交点A、B,连结AC、BC、OC.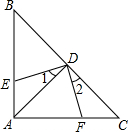 如图,△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点,DE⊥DF,若AB=8cm,则四边形AEDF的面积为( )
如图,△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点,DE⊥DF,若AB=8cm,则四边形AEDF的面积为( )