题目内容
如图，已知∠BAC=30°，G为∠BAC的平分线上的一点，EG∥AC交AB于E，GD⊥AC于D，则GD：GE=________．
1：2
分析：利用角平分线性质，通过作辅助线来求得．
解答：
解：作GN∥AB交AC于点N，
∵G为∠BAC的平分线上的一点，EG∥AC交AB于E，∠BAC=30°，
∴∠EAG=∠AGE=∠GAC=15°
∴AE=EG
∵GN∥AB交AC于点N，
∴GE=GN，∠AGN=15°
∴∠GND=30°
∴在△GND中GD=
GN
即GD=EG．
故答案为1：2．
点评：本题考查了角平分线性质，通过作以辅助线在三角形中来求得．
分析：利用角平分线性质，通过作辅助线来求得．
解答：
解：作GN∥AB交AC于点N，∵G为∠BAC的平分线上的一点，EG∥AC交AB于E，∠BAC=30°，
∴∠EAG=∠AGE=∠GAC=15°
∴AE=EG
∵GN∥AB交AC于点N，
∴GE=GN，∠AGN=15°
∴∠GND=30°
∴在△GND中GD=
GN即GD=
EG．故答案为1：2．
点评：本题考查了角平分线性质，通过作以辅助线在三角形中来求得．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
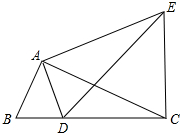如图，已知∠BAC=90°，△ABC绕点A逆时针旋转得到△ADE，恰好D在BC上，连接CE．
如图，已知∠BAC的平分线与△ABC的边BC和外接圆分别相交于D、E．
如图，已知∠BAC=70°，D是△ABC的边BC上的一点，且∠CAD=∠C，∠ADB=80°．求∠B的度数．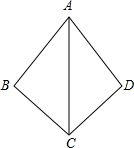
如图，已知∠BAC=∠DAC，要利用“ASA”判定△ABC≌△ADC，则应添加的条件是
如图，已知∠BAC=40°，∠DAC=10°，若将△ABC绕点A逆时针旋转