Question

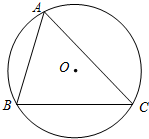
如图，已知∠BAC的平分线与△ABC的边BC和外接圆分别相交于D、E．
求证：AB•AC=AD•AE．

Answer 1

分析：先连接EC，证出∠BAE=∠CAE，∠ABC=∠AEC，得出△ABD∽△AEC，即可得出AB•AC=AD•AE．

解答：解：连接EC，
∵EA是∠BAC的平分线，
∴∠BAE=∠CAE，
∵∠ABC=∠AEC，
∴△ABD∽△AEC，
∴

AB

AE

=

AD

AC

，
∴AB•AC=AD•AE．

点评：此题考查了圆周角定理，关键是根据圆周角定理和已知条件证出△ABD∽△AEC，用到的知识点是圆周角定理、相似三角形的判定与性质．