题目内容
商场销售一批衬衫,每天可售出20件,每件可盈利40元.为了扩大销售,减少库存,决定采取适当的降价措施,经调查发现,如果一件衬衫每降价1元,每天可多售出2件.
(1)设每件降价x元,每天盈利y元,写出y与x之间的函数关系式.
(2)若商场每天要盈利1200元,每件衬衫降价幅度不能超过18元,那么每件衬衫应降价多少元?
(3)每件衬衫降价多少元时,商场每天的盈利能达到最大,盈利最大是多少元?
(1)设每件降价x元,每天盈利y元,写出y与x之间的函数关系式.
(2)若商场每天要盈利1200元,每件衬衫降价幅度不能超过18元,那么每件衬衫应降价多少元?
(3)每件衬衫降价多少元时,商场每天的盈利能达到最大,盈利最大是多少元?
考点:二次函数的应用,一元二次方程的应用
专题:销售问题
分析:(1)商场降价后每天盈利=每件的利润×卖出的件数=(40-降低的价格)×(20+增加的件数),把相关数值代入即可求解;
(2)利用衬衣平均每天售出的件数×每件盈利=每天销售这种衬衣利润列出方程解答即可.
(2)利用衬衣平均每天售出的件数×每件盈利=每天销售这种衬衣利润列出方程解答即可.
解答:解:(1)∵每件衬衫降价1元,商场平均每天可多售出2件,
∴每件衬衫降价x元,商场平均每天可多售出2x件,
∵原来每件的利润为40元,现在降价x元,
∴现在每件的利润为(40-x)元,
∴y=(40-x)(20+2x)=-2x2+60x+800;
(2)设每件衬衫应降价x元.
根据题意,得 (40-x)(20+2x)=1200
整理,得x2-30x+200=0
解得x1=10,x2=20.
∵降价不能超过18元,
∴x2=20应略去,
∴x=10.
答:每件衬衫应降价10元.
(3)∵y=-2x2+60x+800=-2(x-15)+1250,
∴降价15元时有最大利润1250元;
∴每件衬衫降价x元,商场平均每天可多售出2x件,
∵原来每件的利润为40元,现在降价x元,
∴现在每件的利润为(40-x)元,
∴y=(40-x)(20+2x)=-2x2+60x+800;
(2)设每件衬衫应降价x元.
根据题意,得 (40-x)(20+2x)=1200
整理,得x2-30x+200=0
解得x1=10,x2=20.
∵降价不能超过18元,
∴x2=20应略去,
∴x=10.
答:每件衬衫应降价10元.
(3)∵y=-2x2+60x+800=-2(x-15)+1250,
∴降价15元时有最大利润1250元;
点评:考查了二次函数及其应用问题,是中学数学中的重要基础知识之一,是运用数学知识解决现实中的最值问题的常用方法和经典模型;应牢固掌握二次函数的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
-4的倒数是( )
A、-
| ||
B、
| ||
| C、-4 | ||
| D、4 |
△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠ADC的度数是( )
| A、107° | B、112° |
| C、117° | D、122° |
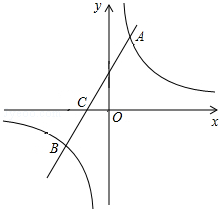 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=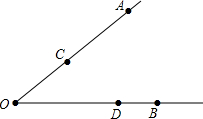 如图,已知点A、点C、点B、点D分别在∠O的边上.
如图,已知点A、点C、点B、点D分别在∠O的边上.