题目内容
4.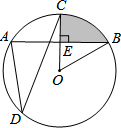 如图,A、B、C、D在⊙O上,OC⊥AB,垂足为E,∠ADC=30°,⊙O的半径为2.求:
如图,A、B、C、D在⊙O上,OC⊥AB,垂足为E,∠ADC=30°,⊙O的半径为2.求:(1)∠BOC的度数;
(2)由BE、CE及弧BC围成的阴影部分面积.
分析 (1)根据垂径定理得到$\widehat{AC}=\widehat{BC}$,根据圆周角定理即可得到结论;
(2)根据三角形的内角和得到∠OBE=30°,解直角三角形得到OE=1,BE=$\sqrt{3}$,根据扇形和三角形的面积公式即可得到结论.
解答 解:(1)∵OC⊥AB,
∴$\widehat{AC}=\widehat{BC}$,
∵∠ADC=30°,
∴∠BOC=2∠ADC=60°,
(2)∵∠BOC=60°,OC⊥AB,
∴∠OBE=30°,
∵⊙O的半径为2,
∴OE=1,BE=$\sqrt{3}$,
∴由BE、CE及弧BC围成的阴影部分面积=S扇形-S△BOE=$\frac{60•π•{2}^{2}}{360}$-$\frac{1}{2}×\sqrt{3}×1$=$\frac{2π}{3}$-$\frac{\sqrt{3}}{2}$.
点评 本题考查了圆周角定理,扇形的面积计算,垂径定理,解直角三角形,正确的识图是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下列计算错误的是( )
| A. | (-1$\frac{1}{2}$)+0.5=-1 | B. | -1÷4×$\frac{1}{4}$=-$\frac{1}{16}$ | C. | $\frac{3^2}{4}$=$\frac{9}{16}$ | D. | -32+(-3)2=0 |
12.如图所示图形是轴对称图形的有( )


| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
19.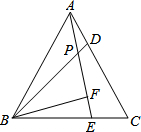 如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )
如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )
 如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )
如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )| A. | 2 | B. | 3 | C. | 1 | D. | 2$\sqrt{3}$ |
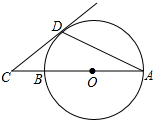 如图所示,AB是⊙O的直径,AD是弦,∠DAB=20°,延长AB到点C,使得∠ACD=
如图所示,AB是⊙O的直径,AD是弦,∠DAB=20°,延长AB到点C,使得∠ACD=