Question

【题目】已知抛物线与轴只有一个公共点，且与轴交于点

(1)试判断该抛物线的开口方向，说明理由；

(2)若，轴交该抛物线于点，且是直角三角形，求抛物线的解析式；

(3)若直线()与该抛物线有两个交点，且与轴和轴分别交于点，记的面积为，求的取值范围

Answer 1

【答案】（1）开口向上；（2）y= ；（3）

【解析】

（1）根据二次函数与一元二次方程的关系，可得到方程的判别式为0，从而得解；

（2）将含有字母系数的解析式化为顶点式，得到点, B（0，2），,在中证得BD=CD=AD从而求得b的值，即可得出函数解析式；

（3）联立方程组并化为一元二次方程，根据有2个交点得到判别式大于0，由此可确定b的取值范围，进一步得到用含b的式子表示的面积表达式，因此可得到的取值范围.

解：（1），y=0时，

∵与x轴只有一个公共点A

∴开口向上；

（2）如图，

，

∴

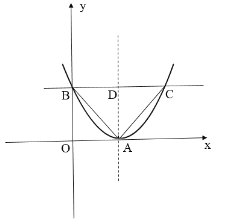
与y轴交点B（0，2），

在中，，

B，C关于AD对称，即BD=CD=AD,

（3）如图

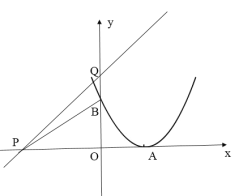
∵与该抛物线有两个交点，

∵x=0时，

y=0时，,

∴,

设

m=1时，S最小值是，m>1时，S随着m的增大而增大，