题目内容
【题目】如图，在Rt△ABC中，∠B＝90°，AB＝20cm，BC＝15cm，动点P从点A出发，以每秒4cm的速度沿AB方向运动，到达点B时停止运动．过点P作AB的垂线交斜边AC于点E，将△APE绕点P顺时针旋转90°得到△DPF．设点P在边AB上运动的时间为t（秒）．
（1）当点F与点B重合时，求t的值；
（2）当△DPF与△ABC重叠部分的图形为四边形时，设此四边形的面积为S，求S与t的函数关系式；
（3）若点M是DF的中点，当点M恰好在Rt△ABC的内角角平分线上时，求t的值.
【答案】（1）
；（2）S=
（0<t≤）；（3）
或
.
【解析】
（1）由条件可得AP=4t，易证
，根据相似三角形的性质可得PE=3t，由旋转的性质可得PE= PF，然后根据PF+AP=AB建立方程，就可求出t的值．
（2）先用t的代数式表示出DE长及
的面积，然后证明
，再求出
的面积，然后运用相似三角形性质（相似三角形的面积比等于相似比的平方）将
的面积用t的代数式表示，就可得到S与t的函数关系式.
（3）设DF交AC于点G，过点M作MH⊥AB于点H，过点M作MN⊥BC于点N，如图3，先分别用t的代数式表示出MG、MH、MN的长，然后运用角平分线的性质建立等量关系，就可求出t的值.
(1) ∵△APE绕点P顺时针旋转90°得到△DPF,
∴∠D=∠A,∠DFP=∠AEP,∠DPB=∠APE=90°,AP=DP,EP=FP,AE=DF,
∵点F与点B重合，
∴PB=PF,
∴EP=BP,
∵AB=20,AP=4t，
∴EP=BP=20-4t，
∵∠APE=∠ABC=90°,
∴PE∥BC,
∴,
∴
,
∵BC=15,AP=4t,AB=20,
∴PE=3t,
∵EP=BP=20-4t,
∴3t=10-4t,
解得：t=,
∴t的值为（秒）；
（2）当与重叠部分的图形为四边形时，如下图：
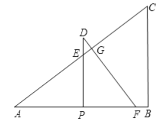
此时0<t≤，
∵PE∥BC,
∴∠DEG=∠C,
又∵∠D=∠A,
∴,
∴
,
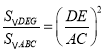∵∠B=90°,AB=20,BC=15,
∴AC=25, 
=
=150,
∵DE=DP-EP=AP-EP=4t-3t=t,
∴
,
∴
=
,
∵
=
=
=
,
∴S=
-=-=,
∴S与t的函数关系式为：S=（0<t≤）.
（3）设DF交AC于点G，过点M做MH⊥AB于点H，过点M作MN⊥BC于点N，如下图：
∵，
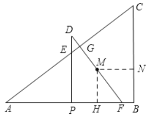
∴∠DGE=∠B=90°, 
,
∵DE=t，AB=20,AC=25,
∴DG=
,
∵∠APE=90°,AP=4t,PE=3t,
∴AE=5t,
∴DF=AE=5t,
∵点M是DF的中点，
∴DM=FM=
DF=
,
∴MG=DM-DG=
=
,
∵∠MHF=∠DPF=90°,
∴MH∥DP,
∴
,
∴
,
∴MH=DP=2t,FH=FP=EP=
,
∴HB=AB-AP-PH=20-4t-=20-
,
∵∠MHB=∠B=∠MNB=90°,
∴四边形MNBH为矩形，
∴MN=HB=20-,
①当点M在∠A的角平分线上时，
∵MG⊥AC,MH⊥AB,
∴MG=MH,
∴=2t，
解得：t=0（舍去）.
②当点M在∠B的角平分线上时，
∵MN⊥BC,MH⊥AB,
∴MH=MN,
∴2t=20- ，
解得：t= ,
③当点M在∠C的角平分线上时，
∵MG⊥AC,MN⊥BC,
∴MG=MN,
∴=20- ,
解得：t= ，
综上所述，当点M恰好在
的内角角平分线上时，t的值为（秒）或（秒）.
