题目内容
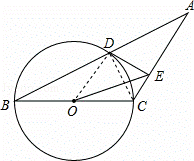
如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.

(1)证明:连接OD,CD,
∵BC为⊙O直径,
∴∠BCD=90°,
即CD⊥AB,
∵△ABC是等腰三角形,
∴AD=BD,
∵OB=OC,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∵D点在⊙O上,
∴DE为⊙O的切线;
(2)解:∵∠A=∠B=30°,BC=4,
∴CD=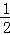 BC=2,BD=BC•cos30°=2
BC=2,BD=BC•cos30°=2 ,
,
∴AD=BD=2 ,AB=2BD=4
,AB=2BD=4 ,
,
∴S△ABC= AB•CD=
AB•CD= ×4
×4 ×2=4
×2=4 ,
,
∵DE⊥AC,
∴DE= AD=
AD= ×2
×2 =
= ,AE=AD•cos30°=3,
,AE=AD•cos30°=3,
∴S△ODE=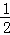 OD•DE=
OD•DE=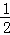 ×2×
×2× =
= ,S△ADE=
,S△ADE=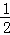 AE•DE=
AE•DE=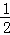 ×
×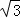 ×3=
×3=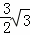 ,
,
∵S△BOD=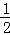 S△BCD=
S△BCD=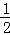 ×
×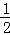 S△ABC=
S△ABC=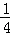 ×4
×4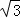 =
=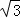 ,
,
∴S△OEC=S△ABC﹣S△BOD﹣S△ODE﹣S△ADE=4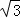 ﹣
﹣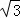 ﹣
﹣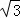 ﹣
﹣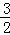
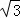 =
=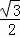 .
.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
从1、2、3、4中任取两个不同的数,其乘积大于4的概率是( )
|
| A. |
| B. |
| C. |
| D. |
|


 ,其中x=1.
,其中x=1.



 ,AC=BC,则▱ABCD的面积是 .
,AC=BC,则▱ABCD的面积是 .
 B.
B.  C.
C.  D. 1
D. 1
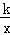 图象上的两点,且x1﹣x2=﹣2,x1•x2=3,y1﹣y2=﹣
图象上的两点,且x1﹣x2=﹣2,x1•x2=3,y1﹣y2=﹣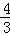 ,当﹣3<x<﹣1时,求y的取值范围.
,当﹣3<x<﹣1时,求y的取值范围. ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+ ;…,按此规律继续旋转,直至得到点P2014为止.则AP2014= .
;…,按此规律继续旋转,直至得到点P2014为止.则AP2014= .