题目内容
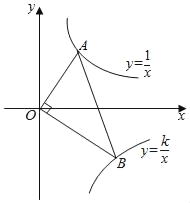
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() ,以
,以![]() 为边在第一象限内作正方形
为边在第一象限内作正方形![]() ,且双曲线
,且双曲线![]() 经过点
经过点![]() .
.
(1)求![]() 的值;
的值;
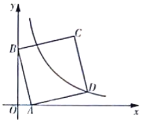
(2)将正方形![]() 沿
沿![]() 轴负方向平移得到正方形
轴负方向平移得到正方形![]() ,当点
,当点![]() 恰好落在双曲线
恰好落在双曲线![]() 上时,求
上时,求![]() 的面积.
的面积.
【答案】(1)5;(2)6.
【解析】
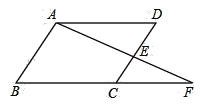
(1)过点D作DE⊥x轴于点E,根据正方形的性质以及角的计算即可证出△OBA≌△EAD(AAS),结合点A、B的坐标即可得出点D的坐标,由点B的坐标利用反比例函数图象上点的坐标特征即可求出反比例函数解析式;
(2)再根据正方形的性质以及点A、B、D的坐标即可得出点C的坐标,由平移可知C与![]() 的纵坐标相同,可求得
的纵坐标相同,可求得![]() 的坐标,从而得到
的坐标,从而得到![]() 的长,即可求出
的长,即可求出![]() 的面积.
的面积.
(1)过点D作DE⊥x轴于点E,如图所示,
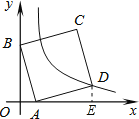
∵四边形ABCD为正方形,
∴∠BAD=90°,AB=AD,
∴∠OAB+∠EAD=90°,
又∵∠OAB+∠OBA=90°,
∴∠OBA=∠EAD,
在△OBA和△EAD中,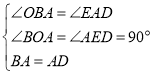 ,
,
∴△OBA≌△EAD(AAS),
∴BO=AE,OA=ED.
∵A(1,0),
∴AO=1,
∵![]() ,
,
∴![]() ,
,
∴AE=BO=4,ED=OA=1,
∴D(5,1),
将D代入![]() ,
,
![]() ,即
,即![]() ;
;
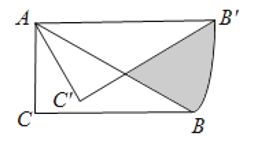
(2)∵A(1,0),B(0,4),且四边形ABCD为正方形,
∴C(4,5),
由![]() 可知
可知![]() ,
,
由平移可知C与![]() 的纵坐标相同,
的纵坐标相同,
在![]() 上,当
上,当![]() 时,
时,![]() ,
,
∴![]() (1,5),
(1,5),![]() ,
,
∵D(5,1),C(4,5),![]() (1,5),
(1,5),
∴D到![]() 的距离为5-1=4,
的距离为5-1=4,
∴![]() .
.

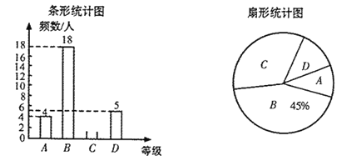
【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A | 0≤t≤0.5 | 6 | 0.15 |
B | 0.5≤t≤1 | a | 0.3 |
C | 1≤t≤1.5 | 10 | 0.25 |
D | 1.5≤t≤2 | 8 | b |
E | 2≤t≤2.5 | 4 | 0.1 |
合计 | 1 |
请根据图表中的信息,解答下列问题:
(1)表中的a= ,b= ,中位数落在 组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.