题目内容

如图，矩形ABCD中，点E在BC的延长线上，BD为对角线，且BD=BE，∠ADB=40°，则∠E的度数是（　　）
A、60°B、70°
C、75°D、80°
考点：矩形的性质,等腰三角形的性质
专题：
分析：根据矩形的对边平行可得AD∥BC，再根据两直线平行，内错角相等可得∠DBC=∠ADB，然后根据等腰三角形两底角相等列式计算即可得解．
解答：解：在矩形ABCD中，AD∥BC，
∴∠DBC=∠ADB=40°，
∵BD=BE，
∴∠E=
1
2
（180°-40°）=70°．
故选B．
点评：本题考查了矩形的对边平行的性质，平行线的性质以及等腰三角形两底角相等的性质，熟记各性质是解题的关键．
练习册系列答案
相关题目
在平面直角坐标系中，△ABC的顶点坐标是A（O，3），B（-3，O），C（-2，O）．点P为△ABC内一点，翻折△ABC得到△A1B1C1（点A、B、C的对应点分别为A1、B1、C1），使点P（m，n）翻折到P′（-m，n）处．
（1）直接写出点A1、B1、C1的坐标；
（2）将△ABC绕点C逆时针旋转90°得到△A2B2C2，画出△A2B2C2；
（3）直接写出点A运动到点A2时所经过的路径长．
已知，如图∠1=∠2，BF=EC，AC=DF．求证：△ABC≌△DEF．
如果-mxny是关于x、y的一个单项式，且系数为3，次数为4，则m=
 
，n=
 
．
计算：
（1）
6
•
12
÷
75
      
 （2）
6
•
12
÷
75

（3）
50
+
8
-4
1
2
+2(
2
-1)0；   
（4）(
9a
+a
1
a
-
2
a
a3
)÷
b
．
⊙O的半径为2，△ABC是⊙O的内接三角形，弧AB所对的圆周角为45°，圆心O到BC的距离为1，则AC的长为
 
．
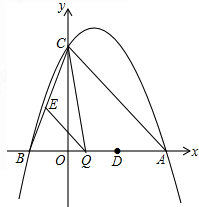已知，如图，抛物线y=ax2-2ax+c（a≠0）与y轴交于点C（0，3），与x轴交于点A、B，点A的坐标为（3，0），点O为坐标原点．
（1）求该抛物线的解析式；
（2）若平行于x轴的动直线l与该抛物线交于点P，与直线AC交于点F，点D的坐标为（2，0）．问：是否存在这样的直线l，使得OF+DF最小？若存在，请求出点P的坐标；若不存在，请说明理由．
（3）点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ．当△CQE的面积最大时，求点Q的坐标．
计算：
（1）
b2
4a2
-
c
a

（2）1-
1
x+1

（3）
a
b
-
b
a
-
a2+b2
ab
．
若点P（m，n）到y轴的距离为3，则下列正确的是（　　）
A、m=3B、n=3
C、m=±3D、n=±3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网