题目内容
如图1,两半径为r的等圆⊙O1和⊙O2相交于M,N两点,且⊙O2过点O1.过M点作直线AB垂直于MN,分别交⊙O1和⊙O2于A,B两点,连接NA,NB.
(1)猜想点O2与⊙O1有什么位置关系,并给出证明;
(2)猜想△NAB的形状,并给出证明;
(3)如图2,若过M的点所在的直线AB不垂直于MN,且点A,B在点M的两侧,那么(2)中的结论是否成立,若成立请给出证明.
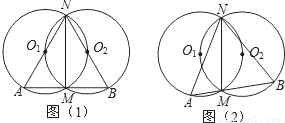
练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
题目内容
如图1,两半径为r的等圆⊙O1和⊙O2相交于M,N两点,且⊙O2过点O1.过M点作直线AB垂直于MN,分别交⊙O1和⊙O2于A,B两点,连接NA,NB.
(1)猜想点O2与⊙O1有什么位置关系,并给出证明;
(2)猜想△NAB的形状,并给出证明;
(3)如图2,若过M的点所在的直线AB不垂直于MN,且点A,B在点M的两侧,那么(2)中的结论是否成立,若成立请给出证明.
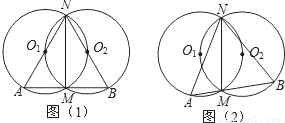
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案