题目内容
1.若函数y=(k-1)x+b+2是正比例函数,则( )| A. | k≠-1,b=-2 | B. | k≠1,b=-2 | C. | k=1,b=-2 | D. | k≠1,b=2 |
分析 根据正比例函数的定义可知k-1≠0,b+2=0,从而可求得k、b的值.
解答 解:∵y=(k-1)x+b+2是正比例函数,
∴k-1≠0,b+2=0.
解得;k≠1,b=-2.
故选:B.
点评 本题主要考查的是正比例函数的定义,根据正比例函数的定义得到k-1≠0,b+2=0是解题的关键.

练习册系列答案
相关题目
12.下列各式中计算错误的是( )
| A. | 2x(2x3+3x-1)=4x4+6x2-2x | B. | b(b2-b+1)=b3-b2+b | ||
| C. | -$\frac{1}{2}x(2{x^2}-2)=-{x^3}$-x | D. | $\frac{2}{3}x(\frac{3}{2}{x^3}-3x+1)={x^4}-2{x^2}+\frac{2}{3}$x |
 如图所示,已知BP为△ABC的角平分线,CD为△ABC的外角∠ACE的平分线,它与BP的延长线交于点D,∠A=70°,求∠D的度数.
如图所示,已知BP为△ABC的角平分线,CD为△ABC的外角∠ACE的平分线,它与BP的延长线交于点D,∠A=70°,求∠D的度数.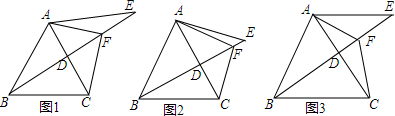
 如图,△ABC和△BDE都是等边三角形,如果∠ABE=40°.那么∠CBD的大小为40°.
如图,△ABC和△BDE都是等边三角形,如果∠ABE=40°.那么∠CBD的大小为40°.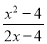 的值为零,则x等于( )
的值为零,则x等于( )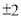 D. 0
D. 0