题目内容
 如图,正△ABC的面积是8,取正△ABC的内心O1,以O1B为边长作正△O1BP1,再取正△O1BP1的内心O2,以O2B为边长作正△O2BP2,…,依次规律作第2009个正△O2009BP2009.则△O2009BP2009的面积是________.
如图,正△ABC的面积是8,取正△ABC的内心O1,以O1B为边长作正△O1BP1,再取正△O1BP1的内心O2,以O2B为边长作正△O2BP2,…,依次规律作第2009个正△O2009BP2009.则△O2009BP2009的面积是________.

分析:根据正三角形的内心和外心重合,则每后一个正三角形的边长是前一个正三角形的外接圆的半径,它们的边长比是
 .再根据相似三角形的面积比是相似比的平方,得每后一个正三角形的面积是前一个正三角形的面积的
.再根据相似三角形的面积比是相似比的平方,得每后一个正三角形的面积是前一个正三角形的面积的 ,所以要求的正三角形的面积是
,所以要求的正三角形的面积是 .
.解答:
 解:如图;
解:如图;Rt△O1BD中,∠O1BD=30°;
∴
 =cos30°=
=cos30°= ;
;∴
 =
= =
= ,
,∴S△O1BP1=
 S△ABC=
S△ABC= ;
;同理可求得S△O2BP2=
 S△O1BP1=
S△O1BP1= ×
× S△ABC=(
S△ABC=( )2×8;
)2×8;依此类推,S△OnBPn=(
 )n×8=
)n×8= ;
;当n=2009时,△O2009BP2009的面积是
 .
.点评:解答此类题一般要先从简单的例子入手得出一般化的结论,然后根据得出的规律去求特定的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为( )
如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为( ) 如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为4,且侧棱AA1⊥底面ABC,其正(主)视图是边长为4的正方形,则此三棱柱侧(左)视图的面积为( )
如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为4,且侧棱AA1⊥底面ABC,其正(主)视图是边长为4的正方形,则此三棱柱侧(左)视图的面积为( )
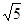 个单位的速度向点C运 动,当一点停止运动,另一点也随之停止,设△CPQ的面 积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围;
个单位的速度向点C运 动,当一点停止运动,另一点也随之停止,设△CPQ的面 积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围;
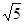 个单位的速度向点C运 动,当一点停止运动,另一点也随之停止,设△CPQ的面
积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围;
个单位的速度向点C运 动,当一点停止运动,另一点也随之停止,设△CPQ的面
积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围;


