题目内容
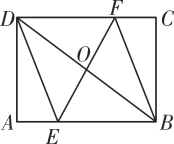
【题目】两块等腰直角三角形纸片![]() 和
和![]() 按图1所示放置,直角顶点重合在点
按图1所示放置,直角顶点重合在点![]() 处,
处,![]() ,
,![]() .保持纸片
.保持纸片![]() 不动,将纸片
不动,将纸片![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]()
![]() .当
.当![]() 与
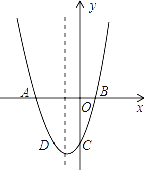
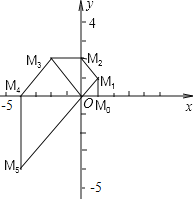
与![]() 在同一直线上(如图2)时,
在同一直线上(如图2)时,![]() 的正切值等于_________.
的正切值等于_________.

【答案】![]()
【解析】
当BD与CD在同一直线上时,根据三角形AOB和COD是等腰直角三角形,可得OA=OB,OC=OD,由旋转可得∠AOC=∠DOB,证明△AOC≌△BOD,可得AC=BD,在RtACB中,设AC=x,则BD=x,根据勾股定理列出方程求出x的值,可得tan∠ABC=![]() =
=![]() ,再根据∠DBO+∠DOB=∠DBO+∠ABC证明∠ABC=α,进而求出α的正切值.
,再根据∠DBO+∠DOB=∠DBO+∠ABC证明∠ABC=α,进而求出α的正切值.
解:当BD与CD在同一直线上(如图2)时,
∵三角形AOB和COD是等腰直角三角形,
∴OA=OB,OC=OD,

由旋转可知:∠AOC=∠DOB=α,
∴△AOC≌△BOD(SAS),
∴AC=BD,∠CAO=∠DBO,
∵∠DBO+∠ABC+∠BAO=90°,
∴∠CAO+∠OAB+∠ABC=90°
∴∠ACB=90°
在RtACB中,设AC=x,则BD=x,
∴BC=CD+BD=4+x,
∵AB=2![]() ,
,
∴根据勾股定理,得x2+(4+x)2=(2![]() )2,
)2,
解得x=2或x=6(舍去),
∴AC=2,BC=6,
∴tan∠ABC=![]() =
=![]() ,
,
∵三角形AOB和COD是等腰直角三角形,
∴∠CDO=∠ABO=45°,
∴∠DBO+∠DOB=∠DBO+∠ABC,
∴∠ABC=∠DOB,
由旋转可知:∠AOC=∠DOB=α,
∴∠ABC=α,
∴tanα=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目