题目内容
8.我国古代把一昼夜划分成十二个时段,每一个时段叫一个时辰,古时与今时的对应关系(部分)如下表所示.天文兴趣小组的小明等4位同学从今夜23:00至明晨7:00将进行接力观测,每人两小时,观测的先后顺序随机抽签确定,小明在子时观测的概率为( )| 古时 | 子时 | 丑时 | 寅时 | 卯时 |
| 今时 | 23:00~1:00 | 1:00~3:00 | 3:00~5:00 | 5:00~7:00 |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
分析 用子时的时间除以观测的总时间即可求得在子时观测的概率.
解答 解:∵从23:00至明晨7:00共8个小时,子时有2小时,
∴小明在子时观测的概率为$\frac{2}{8}$=$\frac{1}{4}$,
故选B.
点评 本题考查概率的求法与运用,一般方法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
13. 如图,点A,B是棱长为1的正方体的两个顶点,将正方体按图中所示展开,则在展开图中A,B两点间的距离为( )
如图,点A,B是棱长为1的正方体的两个顶点,将正方体按图中所示展开,则在展开图中A,B两点间的距离为( )
 如图,点A,B是棱长为1的正方体的两个顶点,将正方体按图中所示展开,则在展开图中A,B两点间的距离为( )
如图,点A,B是棱长为1的正方体的两个顶点,将正方体按图中所示展开,则在展开图中A,B两点间的距离为( )| A. | 2 | B. | $\sqrt{5}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{10}$ |
17.4的相反数是( )
| A. | -4 | B. | 4 | C. | $\frac{1}{4}$ | D. | $-\frac{1}{4}$ |
18.若$\sqrt{m-8}$+|n-2|=0,且关于x的一元二次方程ax2+mx+n=0有实数根,则a的取值范围是( )
| A. | a≥8 | B. | a<8且a≠0 | C. | a≤8 | D. | a≤8且a≠0 |
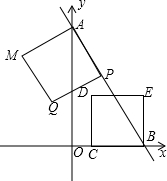 如图,直线y=-$\frac{4}{3}$x+4与坐标轴交于A、B两点,动点P、C以1个单位每秒相同的速度同时分别沿射线AB、BO方向运动,以AP、BC为边分别作如图的两个正方形APQM、BCDE,设动点P的运动时间为t,当正方形APQM的顶点Q落在正方形BCDE的边所在的直线上时,t的值为$\frac{5}{3}$、$\frac{15}{4}$或$\frac{20}{7}$.
如图,直线y=-$\frac{4}{3}$x+4与坐标轴交于A、B两点,动点P、C以1个单位每秒相同的速度同时分别沿射线AB、BO方向运动,以AP、BC为边分别作如图的两个正方形APQM、BCDE,设动点P的运动时间为t,当正方形APQM的顶点Q落在正方形BCDE的边所在的直线上时,t的值为$\frac{5}{3}$、$\frac{15}{4}$或$\frac{20}{7}$.