题目内容
18.若x,y是实数,且$y<\sqrt{x-1}+\sqrt{1-x}+\frac{1}{2}$,求$\frac{|1-y|}{y-1}$的值为-1.分析 根据二次根式有意义的条件可得$\left\{\begin{array}{l}{x-1≥0}\\{1-x≥0}\end{array}\right.$,解不等式组可得x=1,进而可得y$<\frac{1}{2}$,再根据绝对值的性质可得1-y>0,然后化简约分即可.
解答 解:由题意得:$\left\{\begin{array}{l}{x-1≥0}\\{1-x≥0}\end{array}\right.$,
解得:x=1,
则y$<\frac{1}{2}$,
$\frac{|1-y|}{y-1}$=$\frac{1-y}{y-1}$=-1,
故答案为:-1.
点评 此题主要考查了二次根式有意义的条件,以及绝对值的性质,关键是掌握二次根式中的被开方数是非负数.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
13.据报道,投资270亿元的西环高铁预计今年底建成通车,通车后能使西环高铁经过的市县约4360000人受益,数据4360000用科学记数法表示为( )
| A. | 436×104 | B. | 4.36×105 | C. | 4.36×106 | D. | 4.36×107 |
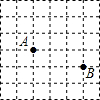 如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都是图中的格点,其中点A、点B的位置如图所示,则点C可能的位置共有( )
如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都是图中的格点,其中点A、点B的位置如图所示,则点C可能的位置共有( ) 如图,直线CD上有一点O,过点O作OA⊥CD,OB平分∠AOD,则∠BOC的度数是135°.
如图,直线CD上有一点O,过点O作OA⊥CD,OB平分∠AOD,则∠BOC的度数是135°.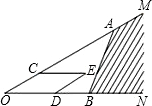 如图,点A、B分别在射线OM、ON上,C、D分别是线段OA和OB上的点,以OC、OD为邻边作平行四边形OCED,下面给出三种作法的条件:
如图,点A、B分别在射线OM、ON上,C、D分别是线段OA和OB上的点,以OC、OD为邻边作平行四边形OCED,下面给出三种作法的条件: