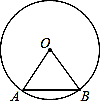题目内容
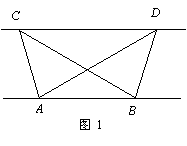
(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置
关系,并说明理由.
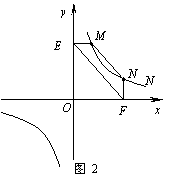
(2)结论应用:① 如图2,点M,N在反比例函数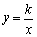 (k>0)的图象上,过点M
(k>0)的图象上,过点M
作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
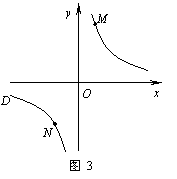
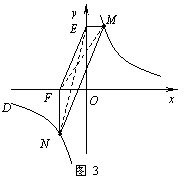
② 若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断 MN与
EF是否平行?请说明理由.
(1)证明:分别过点C,D,作CG⊥AB,DH⊥AB,
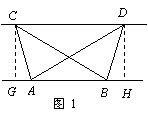 垂足为G,H,则∠CGA=∠DHB=90°.……1分
垂足为G,H,则∠CGA=∠DHB=90°.……1分
∴ CG∥DH.
∵ △ABC与△ABD的面积相等,
∴ CG=DH. …………………………2分
∴ 四边形CGHD为平行四边形.
∴ AB∥CD. ……………………………3分
 (2)①证明:连结MF,NE. …………………4分
(2)①证明:连结MF,NE. …………………4分
设点M的坐标为(x1,y1),点N的坐标为(x2,y2).
∵ 点M,N在反比例函数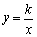 (k>0)的图象上,
(k>0)的图象上,
∴  ,
,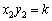 .
.
∵ ME⊥y轴,NF⊥x轴,
 ∴ OE=y1,OF=x2.
∴ OE=y1,OF=x2.
∴ S△EFM=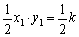 ,
,
S△EFN=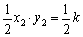 . ………………5分
. ………………5分
∴S△EFM =S△EFN.
由(1)中的结论可知:MN∥EF. ………6分
② MN∥EF. 证明与①类似,略.………7分
(若学生使用其他方法,只要解法正确,皆给分.)

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 的长度?
的长度? 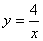 (
(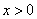 )的图象上,若阴影部分的面积为12 -
)的图象上,若阴影部分的面积为12 -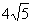 ,则点E的坐标是 .
,则点E的坐标是 . 

 ∥l2∥l3,AB=4,DF=8,BC=6,则DE=__________.
∥l2∥l3,AB=4,DF=8,BC=6,则DE=__________.