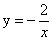题目内容
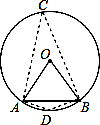
如图,弦AB的长等于⊙O的半径,那么弦AB所对的圆周角的度数是 .
30°或150° .
【考点】圆周角定理;等边三角形的判定与性质.
【分析】首先在优弧上取点C,连接AC,BC,在劣弧AB上取点D,连接AD,BD,由弦AB的长等于⊙O的半径,可得△OAB是等边三角形,然后利用圆周角定理与圆的内接四边形的性质求得答案.
【解答】解:在优弧上取点C,连接AC,BC,在劣弧AB上取点D,连接AD,BD,
∵弦AB的长等于⊙O的半径,
∴△OAB是等边三角形,
∴∠AOB=60°,
∴∠ACB= ∠AOB=30°,
∠AOB=30°,
∴∠ADB=180°﹣∠ACB=150°,
∴弦AB所对的圆周角的度数是:30°或150°.
故答案为:30°或150°.
【点评】此题考查了圆周角定理、圆的内接四边形的性质以及等边三角形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
 (k>0)的图象上,过点M
(k>0)的图象上,过点M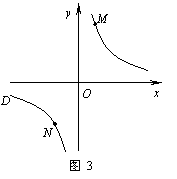
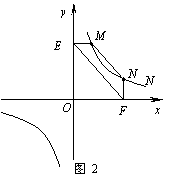
 =5,则a2+
=5,则a2+ 的值是 .
的值是 .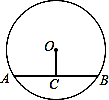


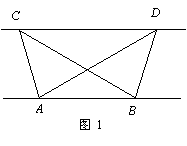
 (k≠0)的图像交于点C,过点C作CB⊥x轴于点B,AO=3BO,
(k≠0)的图像交于点C,过点C作CB⊥x轴于点B,AO=3BO,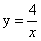 B.
B.
 D.
D.