题目内容
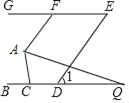
【题目】如图，在平行四边形ABCD中，∠C=120°，AD=2AB=4，点H、G分别是边CD、BC上的动点．连接AH、HG，点E为AH的中点，点F为GH的中点，连接EF．则EF的最大值与最小值的差为（ ）
A. 1 B. 
﹣1 C. 
D. 2﹣
【答案】C
【解析】如图，取AD的中点M，连接CM、AG、AC，作AN⊥BC于N．
∵四边形ABCD是平行四边形，∠BCD=120°，
∴∠D=180°-∠BCD=60°，AB=CD=2，
∵AM=DM=DC=2，
∴△CDM是等边三角形，
∴∠DMC=∠MCD=60°，AM=MC，
∴∠MAC=∠MCA=30°，
∴∠ACD=90°，
∴AC=2
，
在Rt△ACN中，∵AC=2，∠ACN=∠DAC=30°，
∴AN=
AC=，
∵AE=EH，GF=FH，
∴EF=AG，
易知AG的最大值为AC的长，最小值为AN的长，
∴AG的最大值为2，最小值为，
∴EF的最大值为，最小值为
，
∴EF的最大值与最小值的差为．
练习册系列答案
口算题天天练系列答案
相关题目
【题目】棱长为a的小正方体，按照如图所示的方法一直维续摆放，自上而下分别叫第1层、第2层、……第n（n＞0）层，第n层的小方体的个数记为S．
（1）完成下表：
n | 1 | 2 | 3 | 4 | … |
S | 1 | 3 | _____ | _____ | … |
（2）上述活动中，自变量和因变量分别是什么？
（3）研究上表可以发现S随n的增大而增大，且有一定的规律，请你用式子来表示S与n的关系，并计算当n=10时S的值．
