题目内容
14.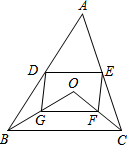 D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC内任意一点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.问当OA与BC应满足怎样的数量关系时,四边形DGFE是菱形,并证明之.
D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC内任意一点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.问当OA与BC应满足怎样的数量关系时,四边形DGFE是菱形,并证明之.
分析 当OA=BC时,四边形DEFG是菱形,选根据三角形中位线定理证明四边形DEFG是平行四边形,再证明EF=FG即可.
解答 解:当OA=BC时,四边形DEFG是菱形.
理由:∵D、E分别是AB、AC的中点,
∴DE∥BC,DE=$\frac{1}{2}$BC,
同理,GF∥BC,FG=$\frac{1}{2}$BC,
∴DE∥FG,DE=GF,
∴四边形DEFG是平行四边形,
连接OA,在△AOC中,E、F分别为AC、OC中点,
∴EF=$\frac{1}{2}$OA,同理在△BOC中,GF=$\frac{1}{2}$BC,
∵OA=BC,
∴EF=GF,
∴OA=BC时,四边形DEFG是菱形.
点评 本题考查菱形的判定、平行四边形的判定和性质、三角形中位线定理等知识,解题的关键是三角形中位线定理的正确运用,属于中考常考题型.

练习册系列答案
相关题目
19.若等腰三角形的底角为40°,则它的顶角度数为( )
| A. | 40° | B. | 100° | C. | 80° | D. | 70° |
6.截止到2015年6月底,济南机动车总保有量为1640000辆,用科学记数法表示这个数为( )
| A. | 16.4×105 | B. | 1.64×105 | C. | 0.164×107 | D. | 1.64×106 |
4.下列各组数中,以它们为边长的线段不能构成直角三角形的是( )
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 2,3,$\sqrt{6}$ | C. | 5,12,13 | D. | $\frac{5}{4}$,1,$\frac{3}{4}$ |
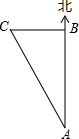 一艘在海上朝正北方向肮行的轮船,从点A到点B航行了240海里时方位仪坏了,凭经验,船长指挥船左转一定角度后,继续航行70海里后到达点C,此时AC之间的距离为250海里,你能判断船转弯后,是否沿正西方向航行?
一艘在海上朝正北方向肮行的轮船,从点A到点B航行了240海里时方位仪坏了,凭经验,船长指挥船左转一定角度后,继续航行70海里后到达点C,此时AC之间的距离为250海里,你能判断船转弯后,是否沿正西方向航行?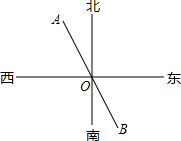 如图所示,已知点A,O,B在同一条直线上,若OA的方向是北偏西26°,则OB的方向是南偏东26°.
如图所示,已知点A,O,B在同一条直线上,若OA的方向是北偏西26°,则OB的方向是南偏东26°.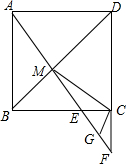 如图,正方形ABCD中,点E是BC上一点,直线AE交BD于点M,交DC的延长线于点F,G是EF的中点,连结CG.求证:
如图,正方形ABCD中,点E是BC上一点,直线AE交BD于点M,交DC的延长线于点F,G是EF的中点,连结CG.求证: