题目内容
10.已知:|ab-2|+(b-1)2=0,求$\frac{1}{ab}$+$\frac{1}{(a+1)(b+1)}$+$\frac{1}{(a+2)(b+2)}$+…+$\frac{1}{(a+2010)(b+2010)}$的值.分析 首先利用非负数的性质得出ab=2,b=1,a=2,代入式子,进一步把分数拆分即可得出答案.
解答 解:∵|ab-2|+(b-1)2=0,
∴ab=2,b=1,a=2,
∴原式=$\frac{1}{2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2011×2012}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2011}$-$\frac{1}{2012}$
=1-$\frac{1}{2012}$
=$\frac{2011}{2012}$.
点评 此题考查代数式求值,非负数的性质,把算式的每一个分数拆成两个分数的差是解决问题的关键.

练习册系列答案
相关题目
20.计算($\sqrt{3}$+2)2013($\sqrt{3}$-2)2014的结果是( )
| A. | 2+$\sqrt{3}$ | B. | $\sqrt{3}$-2 | C. | 2-$\sqrt{3}$ | D. | $\sqrt{3}$ |
2.如图:在某地,人们发现某种蟋蟀1min所叫次数x与当地温度T之间的关系或为T=ax+b,下面蟋蟀所叫次数与温度变化情况对照表:
①根据表中的数据确定a、b的值;
②如果蟋蟀1min叫63次,那么该地当时的温度约为多少摄氏度?
| 蟋蟀叫的次数(x) | … | 84 | 98 | 119 | … |
| 温度(℃)T | … | 15 | 17 | 20 | … |
②如果蟋蟀1min叫63次,那么该地当时的温度约为多少摄氏度?
20.不等式x-1≤1的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
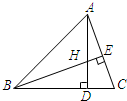 在△ABC中,高AD与BE相交于点H,且AD=BD,问△BHD≌△ACD,为什么?
在△ABC中,高AD与BE相交于点H,且AD=BD,问△BHD≌△ACD,为什么?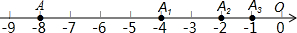 一条数轴如图所示,点A表示的数是-8.
一条数轴如图所示,点A表示的数是-8.