题目内容
已知等腰三角形两腰上的高（或其延长线）相交所成的锐角是50°，求这个三角形的顶角的度数。
解：①高在三角形内部，如图3-1，两高相交所成的锐角∠BOE = 50°，由∠BOE＋∠ABD = ∠A＋∠ABD=90°得∠A = ∠BOE = 50°；
②高在三角形外部，如图3-2，等腰△ABC两腰上的高BE、CD的延长线相交与点O，由∠O＋∠OBD = ∠EAB＋∠ABE = 90°得∠EAB = ∠O = 50°，∠BAC = 130°。
所以顶角度数为50°或130°
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
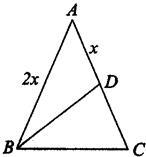22、如图，已知等腰三角形一腰上的中线把三角形周长分为12cm和15cm两部分，求它的底边BC的长．