题目内容
正方体骰子的每个面内都写了一个正整数,随意的投掷这样的两个骰子,若朝上的两个面内的数的和为偶数的概率最小为p,则p= .
考点:列表法与树状图法
专题:
分析:根据题意画出树状图,然后利用概率公式列式计算即可得解.
解答:解:由题意画出树状图如下:

共有36种情况,朝上的两个面内的数的和为偶数的情况共有18种,
所以,P(朝上的两个面内的数的和为偶数)=
=
.
故答案为:
.

共有36种情况,朝上的两个面内的数的和为偶数的情况共有18种,
所以,P(朝上的两个面内的数的和为偶数)=
| 18 |
| 36 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
已知⊙O的直径是11cm,点O到直线m的距离是6cm,则⊙O与直线m的位置关系是( )
| A、相离 | B、相切 |
| C、相交 | D、无法判断 |
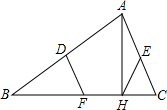 已知:如图,D、E、F分别是△ABC三边中点,AH⊥BC于H,求证:DF=EH.
已知:如图,D、E、F分别是△ABC三边中点,AH⊥BC于H,求证:DF=EH. 如图,在等腰Rt△ABC中,AB=AC=4
如图,在等腰Rt△ABC中,AB=AC=4