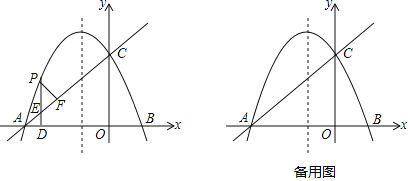Question

【题目】在中，已知．O是上一点，切于A点．

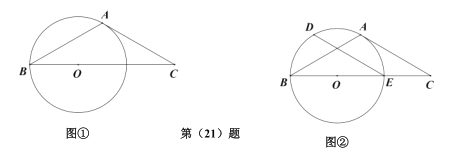
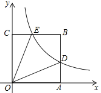
（Ⅰ）如图①，若的半径为6，求线段的长；

（Ⅱ）如图②，交于E点，过E点作交于点D，若，求的长．

Answer 1

【答案】（I）12；（Ⅱ）

【解析】

（1）连接OA，根据等腰三角形的性质，分别得出∠B=∠C,∠B=∠BAO,再结合三角形的外角和内角的关系，得出∠AOC与∠C的关系，根据切线的性质可知△OAC为直角三角形，根据直角三角形中边角关系即可求解.

（2）连接，，由（I）可知，根据圆周角定理推论直径所对的角是直角，可知，根据平行线的性质得到，然后再直角△BED中根据边角关系求出DE的长即可.

解：（I）如图，连接.

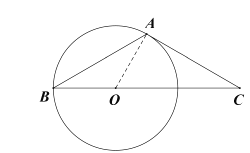
∵为的切线，点A为切点，

∴.

∴∠OAC=90.

∵，

∴.

∴.

∵，

∴.

∴.

∴

∵，

∴

（Ⅱ）如图，

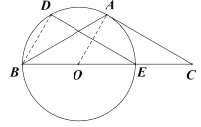
连接，.

由（I）可知，，

∵，

∴

∵，

∴.

∵是直径，

∴.

∵，

∴

在中，，

∴.

∴.