��Ŀ����
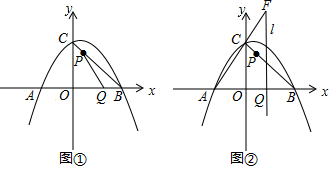
19����ͼ1����ֱ֪��l��y=2x-2�ֱ���x�ᡢy�ύ�ڵ�A��B���㣬CΪl��һ�����ڵ�һ�㣬��AC=2$\sqrt{5}$��������y=ax2+bx-8��A��C���㣬����x�����һ����ΪD����1���������ߵĽ���ʽ��
��2����ͼ2����������y=ax2+bx-8�Ķ���ΪE��PΪֱ��AC�ϵ�һ���㣬��|PD-PE|ֵ���ʱ�����ʱ��P�����꼰|PD-PE|�����ֵ��
��3����ͼ3������MΪx����һ�㣬��NΪƽ����һ�㣬�������Ե�B��C��M��NΪ������ı����Ǿ��Σ���ֱ��д����N�����꣮
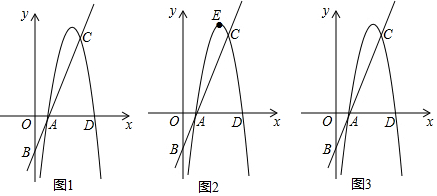
���� ��1�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵ�A�����꣬���������ľ��룬�ɵ�C�����꣬���ݴ���ϵ�������ɵô𰸣�
��2����ͼ2�У���D����ֱ��AC�ĶԳƵ�D�䣬����DD�佻AC��H������DE�ɴ�DE��CC��P����ʱ|PD-EP|��ֵ���
��3���������������ε��ж������ʣ��ɵ�M�����꣬����ƽ���ı��ε����ʣ��ɵô𰸣�
��� �⣺��1����C������Ϊ��m��2m-2����
��y=0ʱ��2x-2=0�����x=1����A��1��0����
��AC=2$\sqrt{5}$����
��m-1��2+��2m-2��2=��2$\sqrt{5}$��2��
���m=3��m=-1���ᣩ��2m-2=4����C��3��4����
��A��C��������뺯������ʽ����
$\left\{\begin{array}{l}{9a+3b-8=4}\\{a+b-8=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-2}\\{b=10}\end{array}\right.$��
�����ߵĽ���ʽΪy=-2x2+10x-8��
��2���䷽����
y=-2��x-$\frac{5}{2}$��2+$\frac{9}{2}$
��E��$\frac{5}{2}$��$\frac{9}{2}$����
��y=0ʱ��=-2x2+10x-8=0�����x=1���ᣩx=4����D������Ϊ��4��0����
��ͼ2�У���D����ֱ��AC�ĶԳƵ�D�䣬����DD�佻AC��H������DE�ɴ�DE��CC��P����ʱ|PD-EP|��ֵ���
��ֱ��DD��Ľ���ʽΪy=-$\frac{1}{2}$x+2��
��$\left\{\begin{array}{l}{y=-\frac{1}{2}x+2}\\{y=2x-2}\end{array}\right.$�ɵ�H��$\frac{8}{5}$��$\frac{6}{5}$����
��D�䣨-$\frac{4}{5}$��$\frac{12}{5}$����
��ֱ��D��E�Ľ���ʽΪy=$\frac{7}{11}$x+$\frac{32}{11}$��
��$\left\{\begin{array}{l}{y=\frac{7}{11}x+\frac{32}{11}}\\{y=2x-2}\end{array}\right.$�ɵ�P��$\frac{18}{5}$��$\frac{26}{5}$����
��ʱ|PD-PE|�����ֵ=D��E=$\sqrt{��\frac{18}{5}-\frac{5}{2}��^{2}-��\frac{26}{5}-\frac{9}{2}��^{2}}$=$\frac{\sqrt{170}}{10}$��
��3����ͼ1 ��
��
��y=0ʱ��2x-2=0�����x=1����D��1��0����
�ߡ�1+��2=90�㣬��2+��3=90�㣬
���1=��3��
�֡ߡ�BOD=��MOB��
���BOD�ס�MOB��
��$\frac{MO}{BO}$=$\frac{BO}{OD}$��
���MO=4����M��-4��0����
�ɶԽ���ƽ�֣���
$\frac{{x}_{N}+{x}_{B}}{2}$=$\frac{{x}_{M}+{x}_{C}}{2}$����$\frac{{x}_{N}+0}{2}$=$\frac{-4+3}{2}$����xN=-1��
$\frac{{y}_{N}+{y}_{B}}{2}$=$\frac{{y}_{M}+{y}_{C}}{2}$����$\frac{{y}_{N}+��-2��}{2}$=$\frac{0+4}{2}$����yN=6��
N��������-1��6����
��ͼ2 ��
��
��CE��OM��E��OE=3��CE=4��
��y=0ʱ��2x-2=0�����x=1����D��1��0����
DE=OE-OD=3-1=2��
�ߡ�1+��2=90�㣬��2+��3=90�㣬
���1=��3��
�֡ߡ�DEC=��CEM��
���DEC�ס�CEM��
��$\frac{DE}{CE}$=$\frac{CE}{EM}$��
���ME=8����M��11��0����
�ɾ��εĶԽ���ƽ�֣���
$\frac{{x}_{N}+{x}_{B}}{2}$=$\frac{{x}_{M}+{x}_{C}}{2}$����$\frac{{x}_{N}+{x}_{C}}{2}$=$\frac{{x}_{B}+{x}_{M}}{2}$��$\frac{{x}_{N}+3}{2}$=$\frac{0+11}{2}$����xN=8��
$\frac{{y}_{N}+{y}_{C}}{2}$=$\frac{{y}_{B}+{y}_{M}}{2}$����$\frac{{y}_{N}+4}{2}$=$\frac{-2+0}{2}$����yN=-6��
N��������8��-6����
��������������MΪx����һ�㣬��NΪƽ����һ�㣬�������Ե�B��C��M��NΪ������ı����Ǿ��Σ���N�����꣨8��-6����-1��6����
���� ���⿼���˶��κ����ۺ��⣬�⣨1���Ĺؼ�����������֮��ľ���ó�C�����꣬�����ô���ϵ�������⣨2���Ĺؼ�������֮��С�ڵ����ߵó�P��DE��AC�Ľ��㣻�⣨3���Ĺؼ����������������ε��ж������ʵó�M������꣬�������˾��ε����ʣ�

 ��������ϵ�д�
��������ϵ�д�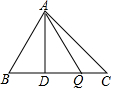 ��ͼ��ʾ����ABC�У���֪BC=16����AD=10������Q��C����CB��B�ƶ��������B�غϣ�����CQ��Ϊx����ACQ�����ΪS����S��x֮��ĺ�����ϵʽΪ��������
��ͼ��ʾ����ABC�У���֪BC=16����AD=10������Q��C����CB��B�ƶ��������B�غϣ�����CQ��Ϊx����ACQ�����ΪS����S��x֮��ĺ�����ϵʽΪ��������| A�� | S=80-5x | B�� | S=5x | C�� | S=10x | D�� | S=5x+80 |
| A�� | a6��a3=a2 | B�� | $\sqrt{6}$��$\sqrt{3}$=$\sqrt{2}$ | C�� | ��-1��-1=1 | D�� | ��a3��2=a5 |
| A�� | 2000�������������һ������ | |
| B�� | ÿ�������Ǹ��� | |
| C�� | ��5������������ѧ�п��ɼ���ȫ�������� | |
| D�� | ͳ���в��õĵ��鷽ʽ���ղ� |
| A�� | 180�� | B�� | 360�� | C�� | 720�� | D�� | 1080�� |
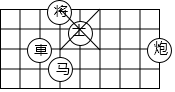 ��ͼ�����̵�һ���֣����ã�1��3����ʾ
��ͼ�����̵�һ���֣����ã�1��3����ʾ ��λ�ã���2��2����ʾ
��λ�ã���2��2����ʾ ��λ�ã���
��λ�ã��� ��λ�ÿɱ�ʾΪ��������
��λ�ÿɱ�ʾΪ��������| A�� | ��1��6�� | B�� | ��6��1�� | C�� | ��6��0�� | D�� | ��7��2�� |
| A�� | 163��103 | B�� | 16.3��104 | C�� | 1.63��105 | D�� | 0.163��106 |
 ��ͼ����������ͬС��������ɵļ�����ĸ���ͼ����ô�������������ǣ�������
��ͼ����������ͬС��������ɵļ�����ĸ���ͼ����ô�������������ǣ�������


