题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 、
、![]() 分别是
分别是![]() 、
、![]() (或它们的延长线)上的动点,且
(或它们的延长线)上的动点,且![]() .
.
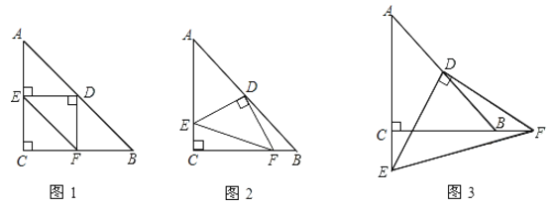
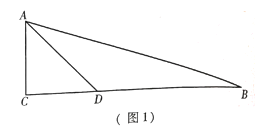
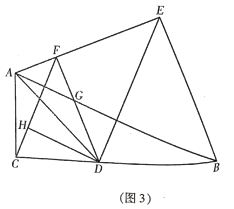
(1)当![]() 时,如图①,线段
时,如图①,线段![]() 和线段
和线段![]() 的关系是:_________________;
的关系是:_________________;
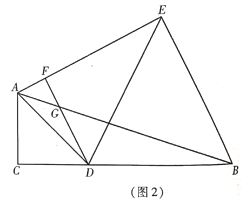
(2)当![]() 与
与![]() 不垂直时,如图②,(1)的结论还成立吗?若成立,请给予证明;若不成立,请说明理由;
不垂直时,如图②,(1)的结论还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3)当![]() 、
、![]() 运动到
运动到![]() 、
、![]() 的延长线时,如图③,请直接写出
的延长线时,如图③,请直接写出![]() 、
、![]() 、
、![]() 之间的关系.
之间的关系.
【答案】(1)![]() ,
,![]() ;(2)成立,证明见解析;(3)
;(2)成立,证明见解析;(3)![]()
【解析】
(1)连接CO,证明△AOM≌△CON可证得OM=ON,∠CON=∠AOM=45°,再证明∠COM=45°即可证明出结论;
(2)连接CO,证明![]() 可证得OM=ON,再证明
可证得OM=ON,再证明![]() 即可得到结论;
即可得到结论;
(3)同(2)得:△OCF≌△OBN,,得出S△OMN=S五边形OBNMC=S△CMN+S△OCB=S△CMN+![]() S△ABC.
S△ABC.
(1)∵![]() ,
,![]() ,
,
∴∠A=45°,
∵![]() ,
,
∴∠AOM=45°,
连接CO,则有CO⊥AB,如图,

∴∠COM=45°,∠BCO=45°,CO=![]() AB
AB
∵![]() 为
为![]() 的中点,
的中点,
∴![]()
∴AO=CO
在△AOM和△CON中

∴△AOM≌△CON
∴OM=ON,∠NOC=∠MOA=45°,
∴∠NOC+∠COM=45°+45°=90°,即![]()
∴![]() ,
,![]()
(2)成立,
证明:连接![]()

![]() ,
,![]()
![]()
![]() ,
,![]() 是
是![]() 中点
中点
![]() ,
,![]() (三线合一)
(三线合一)
![]()
![]()
又![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
(3)![]()
连接CO,如图所示:

同(2)得:△OCF≌△OBN,∠OCM=∠OBN=135°
∴S△OMN=S五边形OBNMC,
=S△CMN+S△OCB,
=S△CMN+![]() S△ABC,
S△ABC,
∴![]() .
.

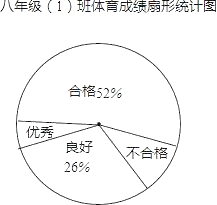
【题目】某校对九年级(1)班全体学生进行体育测试,测试成绩分为优秀、良好、合格和不合格四个等级,根据测试成绩绘制的不完整统计图表如下:
九年级(1)班体育成绩频数分布表:
等级 | 分值 | 频数 |
优秀 | 90﹣100分 | |
良好 | 75﹣89分 | 13 |
合格 | 60﹣74分 | |
不合格 | 0﹣59分 | 9 |
根据统计图表给出的信息,解答下列问题:
(1)九年级(1)班共有多少名学生?
(2)体育成绩为优秀的频数是 ,合格的频数为 ;
(3)若对该班体育成绩达到优秀程度的3个男生和2个女生中随机抽取2人参加学校体育竞赛,恰好抽到1个男生和1个女生的概率是 .
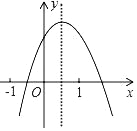
【题目】某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:千帕)随气体体积V(单位:立方米)的变化而变化,p随V的变化情况如表所示.
P | 1.5 | 2 | 2.5 | 3 | 4 | … |
V | 64 | 48 | 38.4 | 32 | 24 | … |
(1)写出一个符合表格数据的p关于V的函数解析式
(2)当气球内的气压大于144千帕时,气球将爆炸,依照(1)中的函数解析式,基于安全考虑,气球的体积至少为多少立方米?