题目内容
3．计算：（1）（a-b）（4a-b）-（a-2b）2+3b2
（2）$\frac{{x}^{2}-8x+16}{{x}^{2}+2x}$÷（$\frac{12}{x+2}$-x+2）
分析 （1）先去括号，然后合并同类项即可解答本题；
（2）根据分式的除法和减法可以解答本题．
解答 解：（1）（a-b）（4a-b）-（a-2b）2+3b2
=4a2-ab-4ab+b2-a2+4ab-4b2+3b2
=3a2-ab；
（2）$\frac{{x}^{2}-8x+16}{{x}^{2}+2x}$÷（$\frac{12}{x+2}$-x+2）
=$\frac{（x-4）^{2}}{x（x+2）}÷\frac{12-（x-2）（x+2）}{x+2}$
=$\frac{（x-4）^{2}}{x（x+2）}•\frac{x+2}{-（x+4）（x-4）}$
=$\frac{4-x}{{x}^{2}+4x}$．
点评 本题考查分式的混合运算、多项式乘多项式、完全平方公式、平方差公式，解答本题的关键是明确它们各自的计算方法．
练习册系列答案
相关题目
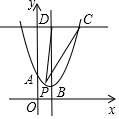如图，在平面直角坐标系中，点A在y轴上，点A、B（$\frac{3}{2}$，m）、C（3，n）均在抛物线y=（x-1）2+1上，点D在抛物线的对称轴上，CD∥x轴．若点P为抛物线上A、B两点间任意一点（包括点A、B），则△PCD面积S的取值范围是3≤S≤$\frac{15}{4}$．
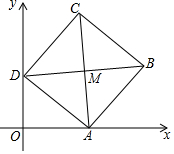在平面直角坐标系中，正方形ABCD的顶点A，D分别在x轴、y轴正半轴上，AC，BD交于点M，若OA=8，OD=6，则点M的坐标为（7，7）．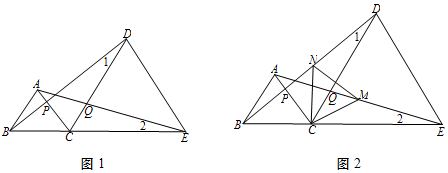
8．今年我市有近5000多名考生参加中考，为了解这些考生的数学成绩，从中抽取300名考生的数学成绩进行统计分析，以下说法正确的是（ ）
| A． | 这300名考生是总体的一个样本 | B． | 近5000多名考生是总体 | ||
| C． | 每位考生的数学成绩是个体 | D． | 300名考生是样本容量 |
如图：在平面直角坐标系中，直线AB与x轴、y轴分别交于B、A两点，若OA、OB的长分别是方程若x2-7mx+48=0的两根且OB＞OA，AB=10．AC平分∠BAO交x轴于点C．