题目内容
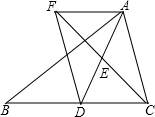
 如图,S正方形ABCD=8,△ADE为等边三角形,F为DE的中点,BE、AF相交于点M,连接DM,则DM=________.
如图,S正方形ABCD=8,△ADE为等边三角形,F为DE的中点,BE、AF相交于点M,连接DM,则DM=________.
2
分析:先根据正方形的面积求出边长AD,再求出EF,然后根据正方形的性质与等边三角形的性质求出∠BAE,AB=AD=AE,再根据等腰三角形两底角相等求出∠AEB=15°,然后求出∠DAM=45°,再根据等边三角形的性质可得AF垂直平分DE,根据线段垂直平分线上的点到线段两端点的距离相等可得DM=EM,再求出△EFM是等腰直角三角形,然后根据等腰直角三角形斜边等于直角边的 倍列式进行计算即可得解.
倍列式进行计算即可得解.
解答:∵S正方形ABCD=8,
∴AD= =2
=2 ,
,
在正方形ABCD和等边△ADE中,
∠BAE=∠BAD+∠DAE=90°+60°=150°,AB=AD=AE,
∴∠AEB= (180°-∠BAE)=
(180°-∠BAE)= (180°-150°)=15°,
(180°-150°)=15°,
∴∠DAM=∠AED-∠AEB=60°-15°=45°,
∵F为DE的中点,
∴AF垂直平分DE,EF= DE=
DE= ×2
×2 =
= ,
,
∴DM=EM,△EFM是等腰直角三角形,
∴EM= EF=
EF= ×
× =2,
=2,
∴DM=2.
故答案为:2.
点评:本题考查了正方形的性质,等边三角形的性质,等腰直角三角形的判定与性质,以及等腰三角形的性质,综合性较强,但难度不大,熟练掌握并灵活运用正方形的性质,等边三角形的性质是解题的关键.
分析:先根据正方形的面积求出边长AD,再求出EF,然后根据正方形的性质与等边三角形的性质求出∠BAE,AB=AD=AE,再根据等腰三角形两底角相等求出∠AEB=15°,然后求出∠DAM=45°,再根据等边三角形的性质可得AF垂直平分DE,根据线段垂直平分线上的点到线段两端点的距离相等可得DM=EM,再求出△EFM是等腰直角三角形,然后根据等腰直角三角形斜边等于直角边的
 倍列式进行计算即可得解.
倍列式进行计算即可得解.解答:∵S正方形ABCD=8,
∴AD=
 =2
=2 ,
,在正方形ABCD和等边△ADE中,
∠BAE=∠BAD+∠DAE=90°+60°=150°,AB=AD=AE,
∴∠AEB=
 (180°-∠BAE)=
(180°-∠BAE)= (180°-150°)=15°,
(180°-150°)=15°,∴∠DAM=∠AED-∠AEB=60°-15°=45°,
∵F为DE的中点,
∴AF垂直平分DE,EF=
 DE=
DE= ×2
×2 =
= ,
,∴DM=EM,△EFM是等腰直角三角形,
∴EM=
 EF=
EF= ×
× =2,
=2,∴DM=2.
故答案为:2.
点评:本题考查了正方形的性质,等边三角形的性质,等腰直角三角形的判定与性质,以及等腰三角形的性质,综合性较强,但难度不大,熟练掌握并灵活运用正方形的性质,等边三角形的性质是解题的关键.

练习册系列答案
相关题目
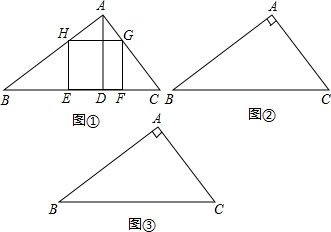
 如图,在△ABC中,DEFG是正方形,D、E在BC边上,G、F分别在AB、AC边上,BC=a,边上的高为h,则正方形DEFG的边长为( )
如图,在△ABC中,DEFG是正方形,D、E在BC边上,G、F分别在AB、AC边上,BC=a,边上的高为h,则正方形DEFG的边长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 8、如图,在△ABC中,点E,D,F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.下列四个判断中,不正确的是( )
8、如图,在△ABC中,点E,D,F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.下列四个判断中,不正确的是( )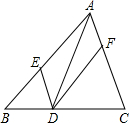 如图,在△ABC中,点D、E、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.下列四种说法:
如图,在△ABC中,点D、E、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.下列四种说法: