题目内容
3. 如图,AB是⊙O的弦,AC是⊙O切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( )
如图,AB是⊙O的弦,AC是⊙O切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( )| A. | 20° | B. | 25° | C. | 40° | D. | 50° |
分析 连接OA,根据切线的性质,即可求得∠C的度数.
解答 解:如图,连接OA,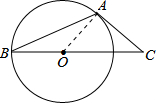
∵AC是⊙O的切线,
∴∠OAC=90°,
∵OA=OB,
∴∠B=∠OAB=20°,
∴∠AOC=40°,
∴∠C=50°.
故选:D.
点评 本题考查了圆的切线性质,以及等腰三角形的性质,掌握已知切线时常用的辅助线是连接圆心与切点是解题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
11.已知等腰三角形的两边长分别为5和6,则这个等腰三角形的周长为( )
| A. | 11 | B. | 16 | C. | 17 | D. | 16或17 |
12. 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:
两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:
①AC⊥BD;②AO=CO=$\frac{1}{2}$AC;③△ABD≌△CBD,
其中正确的结论有( )
 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:
两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=$\frac{1}{2}$AC;③△ABD≌△CBD,
其中正确的结论有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
13.下列运算正确的是( )
| A. | a•a2=a2 | B. | (a2)3=a6 | C. | a2+a3=a6 | D. | a6÷a2=a3 |
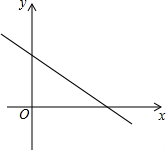 如图,直线l经过点A(4,0),B(0,3).
如图,直线l经过点A(4,0),B(0,3).