题目内容
12. 已知一次函数图象经过点(3,5),(-4,-9)两点.
已知一次函数图象经过点(3,5),(-4,-9)两点.(1)求该一次函数解析式,并画出图象;
(2)求不等式2x-1>0的解集;
(3)若-1<y<1,求x的取值范围.
分析 (1)设一次函数的解析式是y=kx+b,利用待定系数法把(3,5),(-4,-9)代入,可求得函数的解析式;然后根据解析式求出直线与x、y轴的交点,然后画出图象即可;
(2)根据图象可得答案;
(3)利用代入法可得-1<2x-1<1,再解即可.
解答 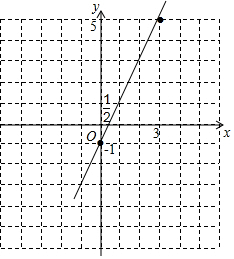 解:(1)设一次函数的解析式是y=kx+b.
解:(1)设一次函数的解析式是y=kx+b.
根据题意得:$\left\{\begin{array}{l}{3k+b=5}\\{-4k+b=-9}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=-1}\end{array}\right.$,
则直线的解析式是:y=2x-1.
(2)由图象可得不等式2x-1>0的解集为x$>\frac{1}{2}$;
(3)∵-1<y<1,
∴-1<2x-1<1,
解得:0<x<1.
点评 此题主要考查了待定系数法求一次函数解析式,以及一次函数与一元一次不等式的关系,关键是正确求出解析式,画出图象.

练习册系列答案
相关题目
11.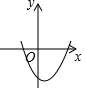 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,以下四个结论:①a>0;②c>0;③b2-4ac>0;④-$\frac{b}{2a}$<0,正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,以下四个结论:①a>0;②c>0;③b2-4ac>0;④-$\frac{b}{2a}$<0,正确的是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,以下四个结论:①a>0;②c>0;③b2-4ac>0;④-$\frac{b}{2a}$<0,正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,以下四个结论:①a>0;②c>0;③b2-4ac>0;④-$\frac{b}{2a}$<0,正确的是( )| A. | ①② | B. | ②④ | C. | ①③ | D. | ③④ |
4.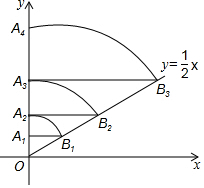 如图,直线l:y=$\frac{1}{2}$x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y 轴于点A3,…,按此做法进行下去,OA2017的长为( )
如图,直线l:y=$\frac{1}{2}$x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y 轴于点A3,…,按此做法进行下去,OA2017的长为( )
 如图,直线l:y=$\frac{1}{2}$x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y 轴于点A3,…,按此做法进行下去,OA2017的长为( )
如图,直线l:y=$\frac{1}{2}$x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y 轴于点A3,…,按此做法进行下去,OA2017的长为( )| A. | ($\sqrt{5}$)2016 | B. | ($\sqrt{5}$)2017 | C. | 22016 | D. | 22017 |
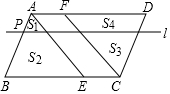 点E、F分别在平行四边形ABCD的边BC、AD上,BE=DF,点P在边AB上,AP:PB=1:n(n>1),过点P且平行于AD的直线l将△ABE分成面积为S1、S2的两部分,将△CDF分成面积为S3、S4的两部分(如图),下列四个等式:
点E、F分别在平行四边形ABCD的边BC、AD上,BE=DF,点P在边AB上,AP:PB=1:n(n>1),过点P且平行于AD的直线l将△ABE分成面积为S1、S2的两部分,将△CDF分成面积为S3、S4的两部分(如图),下列四个等式:


