��Ŀ����
13��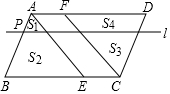 ��E��F�ֱ���ƽ���ı���ABCD�ı�BC��AD�ϣ�BE=DF����P�ڱ�AB�ϣ�AP��PB=1��n��n��1��������P��ƽ����AD��ֱ��l����ABE�ֳ����ΪS1��S2�������֣�����CDF�ֳ����ΪS3��S4�������֣���ͼ���������ĸ���ʽ��
��E��F�ֱ���ƽ���ı���ABCD�ı�BC��AD�ϣ�BE=DF����P�ڱ�AB�ϣ�AP��PB=1��n��n��1��������P��ƽ����AD��ֱ��l����ABE�ֳ����ΪS1��S2�������֣�����CDF�ֳ����ΪS3��S4�������֣���ͼ���������ĸ���ʽ����S1��S3=1��n
��S1��S4=1����2n+1��
�ۣ�S1+S4������S2+S3��=1��n
�ܣ�S3-S1������S2-S4��=n����n+1��
���������������
| A�� | �٢ڢ� | B�� | �ڢ� | C�� | �ڢۢ� | D�� | �ۢ� |
���� ����ƽ���ߵ����ʣ����������ε����ʿ�֪$\frac{{S}_{1}}{{S}_{1}+{S}_{2}}$=��$\frac{1}{n+1}$��2��S3=n2S1��$\frac{{S}_{3}}{{S}_{3}+{S}_{4}}$=��$\frac{n}{n+1}$��2�����S2��S3��S4����S1��n��ʾ�������ɽ�����⣮
��� �⣺�������AP��PB=1��n��n��1����AD��l��BC��
��$\frac{{S}_{1}}{{S}_{1}+{S}_{2}}$=��$\frac{1}{n+1}$��2��S3=n2S1��$\frac{{S}_{3}}{{S}_{3}+{S}_{4}}$=��$\frac{n}{n+1}$��2��
�����ã�S2=n��n+2��S1��S4=��2n+1��S1��
��S1��S4=1����2n+1�����ʢٴ�����ȷ��
�ࣨS1+S4������S2+S3��=[S1+��2n+1��S1]��[n��n+2��S1+n2S1]=1��n���ʢ���ȷ��
�ࣨS3-S1������S2-S4��=[n2S1-S1]��[n��n+2��S1-��2n+1��S1]=1��1���ʢܴ���
��ѡB��
���� ���⿼��ƽ���ı��ε����ʣ����������ε����ʵ�֪ʶ������Ĺؼ���ѧ�����ò���������⣬�����п�ѡ�����е�ѹ���⣮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
4���������꼶������4500��ѧ���μӱ��ο��ԣ�Ҫ���˽���4500��ѧ������ѧ�ɼ����г�ȡ��500����������ѧ�ɼ�����ͳ�Ʒ���������˵����ȷ���ǣ�������
| A�� | ��500�������������һ������ | B�� | ÿλ�����Ǹ��� | ||
| C�� | 500������������ | D�� | ���ֵ����dz������� |
8����һ����ֵ10Ԫ������Ҷһ���1Ԫ��2Ԫ����Ǯ���һ������У�������
| A�� | 9�� | B�� | 8�� | C�� | 7�� | D�� | 6�� |
2��Ҫ��һ����ֵ20Ԫ������һ�����Ǯ�������㹻����ֵΪ1Ԫ��5Ԫ����ң���ô���У�������
| A�� | 2�ֻ��� | B�� | 3�ֻ��� | C�� | 4�ֻ��� | D�� | 5�ֻ��� |
 ��ͼ��ʾ�dz������ƽ��չ��ͼ����AB=x����AD=4x��AN=3x��
��ͼ��ʾ�dz������ƽ��չ��ͼ����AB=x����AD=4x��AN=3x�� ��֪һ�κ���ͼ���㣨3��5������-4��-9�����㣮
��֪һ�κ���ͼ���㣨3��5������-4��-9�����㣮