题目内容
 如图所示,在矩形ABCD中,BC=3AB,E、F是BC边的三等分点,连接AE,AF,AC.请问图中是否存在非全等的相似三角形,并指出.
如图所示,在矩形ABCD中,BC=3AB,E、F是BC边的三等分点,连接AE,AF,AC.请问图中是否存在非全等的相似三角形,并指出.考点:相似三角形的判定,矩形的性质
专题:
分析:先由矩形的性质得出∠B=90°,设AB=k,则BC=3AB=3k,根据三等分点的定义得出BE=EF=FC=
BC=k,由勾股定理,求出AE=
=
k,AF=
=
k,AC=
=
k,再通过计算得到
=
=
,从而判定△EAF∽△ECA.
| 1 |
| 3 |
| AB2+BE2 |
| 2 |
| AB2+BF2 |
| 5 |
| AB2+BC2 |
| 10 |
| AE |
| CE |
| AF |
| CA |
| EF |
| EA |
解答:解:图中存在非全等的相似三角形,是△EAF∽△ECA.理由如下:
∵四边形ABCD是矩形,
∴∠B=90°.
设AB=k,则BC=3AB=3k.
∵E、F是BC边的三等分点,
∴BE=EF=FC=
BC=k.
由勾股定理,得AE=
=
k,
AF=
=
k,
AC=
=
k.
在△EAF与△ECA中,
∵
=
=
,
=
=
,
=
=
,
∴
=
=
,
∴△EAF∽△ECA.
∵四边形ABCD是矩形,
∴∠B=90°.
设AB=k,则BC=3AB=3k.
∵E、F是BC边的三等分点,
∴BE=EF=FC=
| 1 |
| 3 |
由勾股定理,得AE=
| AB2+BE2 |
| 2 |
AF=
| AB2+BF2 |
| 5 |
AC=
| AB2+BC2 |
| 10 |
在△EAF与△ECA中,
∵
| AE |
| CE |
| ||
| 2k |
| ||
| 2 |
| AF |
| CA |
| ||
|
| ||
| 2 |
| EF |
| EA |
| k | ||
|
| ||
| 2 |
∴
| AE |
| CE |
| AF |
| CA |
| EF |
| EA |
∴△EAF∽△ECA.
点评:本题考查了相似三角形的判定,难度适中.判定两三角形相似的方法有:
(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;
(2)三边法:三组对应边的比相等的两个三角形相似;
(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
(4)两角法:有两组角对应相等的两个三角形相似.
同时考查了矩形的性质及勾股定理.
(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;
(2)三边法:三组对应边的比相等的两个三角形相似;
(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
(4)两角法:有两组角对应相等的两个三角形相似.
同时考查了矩形的性质及勾股定理.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
不等式
x<6的解集在数轴上表示正确的是( )
| 2 |
| 3 |
A、 |
B、 |
C、 |
D、 |
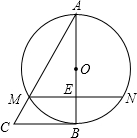 如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=1,AM=2,AE=
如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=1,AM=2,AE=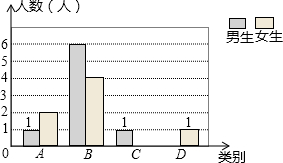 某校九年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如下图表:
某校九年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如下图表: 如图,在△ABC中,∠ABC、∠ACB的平分线交于点O.
如图,在△ABC中,∠ABC、∠ACB的平分线交于点O.