Question

如图，直线l经过原点和点A（3，5），点B在x轴的正半轴上，且∠ABO=45°，AH⊥OB，垂足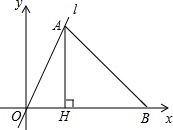为点H．
（1）求直线l所对应的函数解析式；
（2）求线段AH、OB的长度之比；
（3）如果点P是线段OB上一点，设BP=x，△APB的面积为S，写出S与x的函数关系式，并指出自变量x的取值范围．当x取何值时，∠APB为钝角．

Answer 1

分析：（1）设直线l的函数解析式是y=kx（k≠0）．然后利用已知条件可以得到关于k的方程，解方程即可求解；
（2）由A（3，5），AH⊥OB可以得到AH=5，OH=3，而∠ABO=45°，且∠AHB=90°，可以得到AH和OB的长度解决问题；
（3）根据（2）知道∠ABO=45°，所以AH是△APB的高，然后利用三角形的面积公式即可求解．

解答：解：（1）根据题意，设直线l的函数解析式是y=kx（k≠0）．
∵点A（3，5）在直线l上
∴k=

5

3

．
∴y=

5

3

x．（2分）

（2）∵A（3，5），AH⊥OB，
∴AH=5，OH=3．
∵∠ABO=45°，且∠AHB=90°，
∴BH=AH=5．
∴OB=OH+BH=8，
AH：OB=5：8；

（3）S=5x（0＜x≤8）．（2分）
当3＜x＜8时，∠APB为钝角．（1分）

点评：此题主要考查了一次函数的综合题，解题时首先利用待定系数法确定函数解析式，然后利用图象的几何性质即可解决问题．