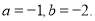题目内容
如图,抛物线y=ax2+2ax+c的图象与x轴交于A、B两点(点A在点B的左边)AB=4,与y轴交于点C,OC=OA,点D为抛物线的顶点.
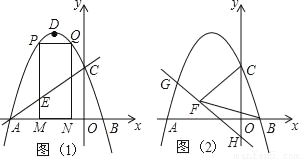
(1)求抛物线的解析式;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM,如图1,点P在点Q左边,当矩形PQNM的周长最大时,求m的值,并求出此时的△AEM的面积;
(3)已知H(0,﹣1),点G在抛物线上,连HG,直线HG⊥CF,垂足为F,若BF=BC,求点G的坐标.
(1)y=﹣x2﹣2x+3; (2)m=﹣2, ; (3)点G的坐标为(, )或(, ). 【解析】试题分析:(1)根据抛物线y=ax2+2ax+c,可得C(0,c),对称轴为x﹣1,再根据OC=OA,AB=4,可得A(﹣3,0),最后代入抛物线y=ax2+2ax+3,得抛物线的解析式为y=﹣x2﹣2x+3; (2)根据点M(m,0),可得矩形PQNM中,P(m,﹣m2﹣2m+3...
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
身高相等的三名同学甲,乙,丙参加风筝比赛,三人放出风筝的线长,线与地面夹角如下表(假设风筝线是拉直的),则三人所放的风筝中( )
同 学 | 甲 | 乙 | 丙 |
放出风筝线长 | 100m | 100m | 90m |
线与地面交角 | 40° | 45° | 60° |
A. 甲的最高 B. 丙的最高 C. 乙的最低 D. 丙的最低
B 【解析】试题解析:由题意可知,甲、乙、丙三人所放风筝的高分别为100sin 40m,100sin 45° m,90sin 60m. 丙所放的风筝最高. 故选B.

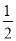 ∠AOC,则∠BOC=____.
∠AOC,则∠BOC=____.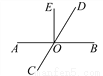
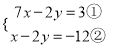 有以下步骤:(1)由①,得2y=7x-3③;(2)把③代入①,得7x-7x-3=3;(3)整理,得3=3;(4)∴x可取一切有理数,原方程组有无数组解.以上解法造成错误步骤是( )
有以下步骤:(1)由①,得2y=7x-3③;(2)把③代入①,得7x-7x-3=3;(3)整理,得3=3;(4)∴x可取一切有理数,原方程组有无数组解.以上解法造成错误步骤是( ) .
.
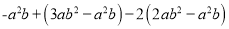 ,其中
,其中